6 Ways to Master Surface Area in Grade 6
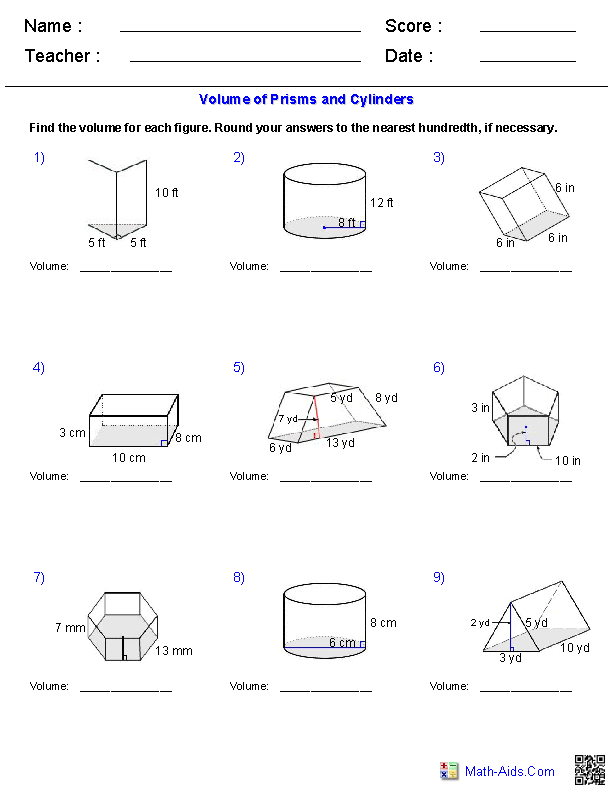
Understanding Surface Area: A Comprehensive Guide for Grade 6 Students
As a Grade 6 student, you’re probably familiar with the concept of area and perimeter. However, when it comes to 3D objects, things can get a bit more complicated. That’s where surface area comes in – the total area of all the surfaces of a 3D object. In this post, we’ll explore six ways to master surface area, making it easier for you to understand and calculate.
1. Start with the Basics: Define Surface Area
Before diving into calculations, it’s essential to understand what surface area is. Surface area is the total area of all the surfaces of a 3D object. Think of it as the amount of wrapping paper needed to cover a gift box. The more complex the shape, the more challenging it is to calculate the surface area.
2. Identify the Type of 3D Object
There are several types of 3D objects, including:
- Rectangular prisms (e.g., a shoe box)
- Triangular prisms (e.g., a roof)
- Cylinders (e.g., a can of soda)
- Spheres (e.g., a basketball)
Each type of object has its own formula for calculating surface area. Familiarize yourself with these formulas to make calculations easier.
3. Use Formulas to Calculate Surface Area
Here are the formulas for calculating surface area for each type of 3D object:
- Rectangular prism: 2(lw + lh + wh)
- Triangular prism: 2 × (base area + height × side length)
- Cylinder: 2πrh + 2πr^2
- Sphere: 4πr^2
Where:
- l = length
- w = width
- h = height
- r = radius
- π = pi (approximately 3.14)
Practice using these formulas to calculate the surface area of different objects.
4. Visualize and Break Down Complex Shapes
When dealing with complex shapes, it’s helpful to break them down into simpler shapes. Visualize the object as a combination of rectangles, triangles, and other basic shapes. Calculate the surface area of each individual shape, then add them up to find the total surface area.
5. Use Real-World Examples to Practice
Practice makes perfect! Use real-world examples to practice calculating surface area. For instance:
- Wrapping a gift: Calculate the surface area of a rectangular prism (the gift box) to determine how much wrapping paper you’ll need.
- Painting a room: Calculate the surface area of the walls, floor, and ceiling to determine how much paint you’ll need.
6. Create a Cheat Sheet or Formula Chart
Create a cheat sheet or formula chart to help you remember the different formulas for calculating surface area. This will come in handy when you’re working on problems or taking a test.
📝 Note: Make sure to label each formula clearly and include examples to help you understand how to apply them.
| Object | Formula | Example |
|---|---|---|
| Rectangular prism | 2(lw + lh + wh) | 2(5 × 3 + 5 × 2 + 3 × 2) = 2(15 + 10 + 6) = 2(31) = 62 |
| Triangular prism | 2 × (base area + height × side length) | 2 × (12 + 5 × 4) = 2 × (12 + 20) = 2 × 32 = 64 |
| Cylinder | 2πrh + 2πr^2 | 2 × 3.14 × 4 × 5 + 2 × 3.14 × 4^2 = 251.2 + 100.5 = 351.7 |
| Sphere | 4πr^2 | 4 × 3.14 × 5^2 = 314 |
By following these six steps, you’ll become a master of surface area in no time. Remember to practice regularly and use real-world examples to make the concept more relatable.
In summary, mastering surface area requires a solid understanding of the formulas and the ability to apply them to different types of 3D objects. With practice and patience, you’ll be able to calculate surface area with ease and confidence.
What is the difference between surface area and volume?
+Surface area is the total area of all the surfaces of a 3D object, while volume is the amount of space inside the object.
How do I calculate the surface area of a triangular prism?
+The formula for calculating the surface area of a triangular prism is 2 × (base area + height × side length).
What is the surface area of a sphere with a radius of 4 cm?
+The surface area of a sphere with a radius of 4 cm is 4πr^2 = 4 × 3.14 × 4^2 = 201.06 cm^2.
Related Terms:
- Surface area worksheet with answers
- Surface area nets worksheet pdf
- Area 6th grade worksheets