6 Ways to Calculate Surface Area of Prisms and Pyramids
Calculating the surface area of three-dimensional shapes like prisms and pyramids is an essential skill in geometry and engineering. In this article, we will explore six different methods to calculate the surface area of these shapes, including rectangular prisms, triangular prisms, square pyramids, and more.
Understanding the Basics
Before diving into the calculations, let’s review the basic concepts. The surface area of a three-dimensional shape is the total area of all its faces. For prisms and pyramids, this includes the area of the base and the lateral (side) faces.
Key Formulas:
- Rectangular prism: SA = 2lw + 2lh + 2wh
- Triangular prism: SA = bh + 3sl
- Square pyramid: SA = b^2 + 4(1⁄2)bs
Where: SA = surface area l = length w = width h = height b = base side length s = slant height
1. Rectangular Prism Surface Area
A rectangular prism has six rectangular faces. To calculate its surface area, you need to find the area of each face and add them up.
Step-by-Step Instructions:
- Find the length (l), width (w), and height (h) of the prism.
- Calculate the area of each face:
- Top and bottom faces: lw
- Front and back faces: lh
- Left and right faces: wh
- Add up the areas of all six faces: SA = 2lw + 2lh + 2wh
Example: Find the surface area of a rectangular prism with length 6 cm, width 4 cm, and height 8 cm.
SA = 2(6 × 4) + 2(6 × 8) + 2(4 × 8) SA = 48 + 96 + 64 SA = 208 cm^2
2. Triangular Prism Surface Area
A triangular prism has five faces: two triangular faces and three rectangular faces. To calculate its surface area, you need to find the area of each face and add them up.
Step-by-Step Instructions:
- Find the base side length (b), height (h), and slant height (s) of the prism.
- Calculate the area of each face:
- Triangular faces: (1⁄2)bh
- Rectangular faces: sl
- Add up the areas of all five faces: SA = bh + 3sl
Example: Find the surface area of a triangular prism with base side length 5 cm, height 6 cm, and slant height 8 cm.
SA = (5 × 6) + 3(5 × 8) SA = 30 + 120 SA = 150 cm^2
3. Square Pyramid Surface Area
A square pyramid has five faces: a square base and four triangular faces. To calculate its surface area, you need to find the area of each face and add them up.
Step-by-Step Instructions:
- Find the base side length (b) and slant height (s) of the pyramid.
- Calculate the area of each face:
- Square base: b^2
- Triangular faces: (1⁄2)bs
- Add up the areas of all five faces: SA = b^2 + 4(1⁄2)bs
Example: Find the surface area of a square pyramid with base side length 4 cm and slant height 6 cm.
SA = 4^2 + 4(1⁄2)(4 × 6) SA = 16 + 48 SA = 64 cm^2
4. Lateral Surface Area of a Prism
The lateral surface area of a prism is the total area of its side faces, excluding the top and bottom faces.
Step-by-Step Instructions:
- Find the length (l), width (w), and height (h) of the prism.
- Calculate the area of each side face:
- Front and back faces: lh
- Left and right faces: wh
- Add up the areas of all side faces: LSA = 2lh + 2wh
Example: Find the lateral surface area of a rectangular prism with length 6 cm, width 4 cm, and height 8 cm.
LSA = 2(6 × 8) + 2(4 × 8) LSA = 96 + 64 LSA = 160 cm^2
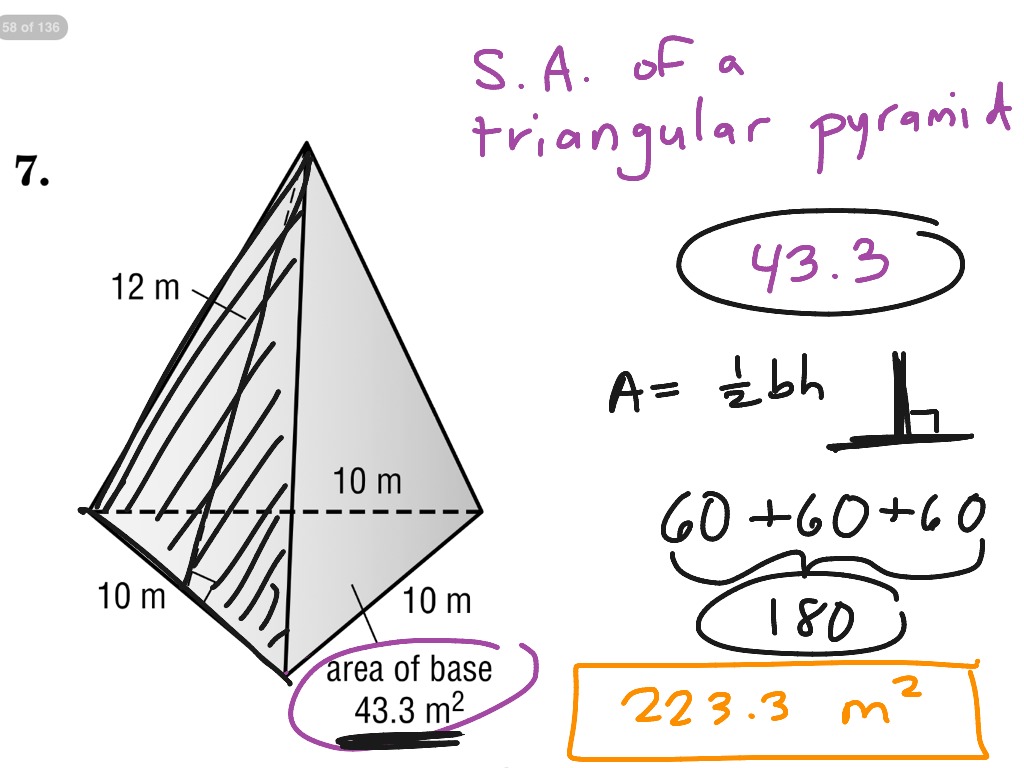
5. Surface Area of a Triangular Pyramid
A triangular pyramid has four faces: a triangular base and three triangular faces. To calculate its surface area, you need to find the area of each face and add them up.
Step-by-Step Instructions:
- Find the base side length (b), height (h), and slant height (s) of the pyramid.
- Calculate the area of each face:
- Triangular base: (1⁄2)bh
- Triangular faces: (1⁄2)bs
- Add up the areas of all four faces: SA = (1⁄2)bh + 3(1⁄2)bs
Example: Find the surface area of a triangular pyramid with base side length 5 cm, height 6 cm, and slant height 8 cm.
SA = (1⁄2)(5 × 6) + 3(1⁄2)(5 × 8) SA = 15 + 60 SA = 75 cm^2
6. Using Formulas and Tables
For more complex shapes or when working with multiple shapes, it can be helpful to use formulas and tables to streamline your calculations.
Table:

| Shape | Formula |
|---|---|
| Rectangular Prism | SA = 2lw + 2lh + 2wh |
| Triangular Prism | SA = bh + 3sl |
| Square Pyramid | SA = b^2 + 4(1⁄2)bs |
| Lateral Surface Area | LSA = 2lh + 2wh |
Example: Find the surface area of a rectangular prism with length 8 cm, width 6 cm, and height 10 cm, using the formula table.
SA = 2(8 × 6) + 2(8 × 10) + 2(6 × 10) SA = 96 + 160 + 120 SA = 376 cm^2
By using these formulas and tables, you can quickly and accurately calculate the surface area of various prisms and pyramids.
📝 Note: Always check your units and ensure that you are using the correct formulas and values to get accurate results.
In conclusion, calculating the surface area of prisms and pyramids is a crucial skill in geometry and engineering. By mastering these six methods and using formulas and tables, you can efficiently and accurately calculate the surface area of various shapes.
What is the formula for the surface area of a rectangular prism?
+SA = 2lw + 2lh + 2wh
How do I calculate the lateral surface area of a prism?
+LSA = 2lh + 2wh
What is the formula for the surface area of a triangular pyramid?
+SA = (1⁄2)bh + 3(1⁄2)bs



