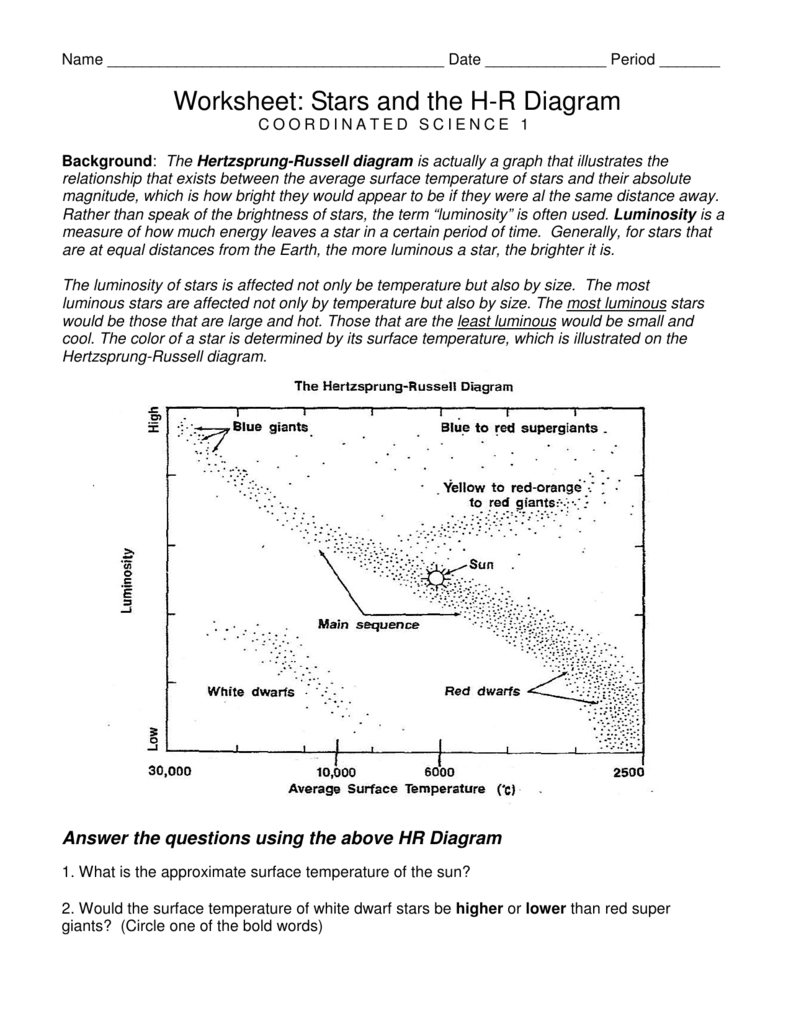
Surface Area of a Rectangular Prism Made Easy

Unlocking the Secrets of Rectangular Prism Surface Area

Calculating the surface area of a rectangular prism can seem daunting at first, but with the right approach, it can be a breeze. In this comprehensive guide, we’ll break down the concept, explore the formula, and provide step-by-step examples to help you master this essential math skill.

What is a Rectangular Prism?

A rectangular prism, also known as a rectangular box or cuboid, is a three-dimensional solid object with six faces, each of which is a rectangle. It has three dimensions: length, width, and height. Understanding the properties of a rectangular prism is crucial for calculating its surface area.

What is Surface Area?

Surface area is the total area of the surface of a three-dimensional object. In the case of a rectangular prism, it’s the sum of the areas of all six faces. The surface area of a rectangular prism can be calculated using a simple formula, which we’ll explore next.

The Formula: Surface Area of a Rectangular Prism

The formula for calculating the surface area of a rectangular prism is:

SA = 2lw + 2lh + 2wh

Where:

• SA = Surface Area
• l = Length
• w = Width
• h = Height

This formula calculates the surface area by adding the areas of all six faces:

• 2lw (top and bottom faces)
• 2lh (front and back faces)
• 2wh (left and right faces)

Step-by-Step Examples

Let’s apply the formula to some examples to illustrate how it works.

Example 1:

Find the surface area of a rectangular prism with a length of 6 cm, a width of 4 cm, and a height of 3 cm.

• SA = 2lw + 2lh + 2wh
• SA = 2(6)(4) + 2(6)(3) + 2(4)(3)
• SA = 48 + 36 + 24
• SA = 108 cm²

Example 2:

Find the surface area of a rectangular prism with a length of 8 m, a width of 5 m, and a height of 2 m.

• SA = 2lw + 2lh + 2wh
• SA = 2(8)(5) + 2(8)(2) + 2(5)(2)
• SA = 80 + 32 + 20
• SA = 132 m²

Tips and Tricks

Here are some additional tips to help you master the concept of surface area:

• Make sure to label your dimensions correctly: length, width, and height.
• Double-check your calculations to avoid errors.
• Use real-world examples to practice calculating surface area.
• Visualize the rectangular prism to help you understand the concept of surface area.

📝 Note: Remember to include units in your calculations (e.g., cm², m²) to ensure accuracy.

Real-World Applications

Calculating the surface area of a rectangular prism has numerous real-world applications, such as:

• Architecture: designing buildings and structures
• Engineering: designing and optimizing systems
• Packaging: calculating the surface area of boxes and containers
• Art: creating sculptures and installations

Common Mistakes to Avoid

Here are some common mistakes to avoid when calculating the surface area of a rectangular prism:

• Forgetting to include the areas of all six faces
• Mixing up the dimensions (length, width, and height)
• Not labeling units correctly

🚨 Note: Double-check your calculations to avoid these common mistakes.

Conclusion

Mastering the surface area of a rectangular prism requires practice and patience. By understanding the formula, applying it to examples, and following tips and tricks, you’ll become proficient in calculating the surface area of rectangular prisms. Remember to visualize the concept, label your dimensions correctly, and avoid common mistakes.

Related Terms:

• Volume of rectangular prism Worksheet