Cylinder Surface Area Worksheet for Students

Understanding Cylinder Surface Area: A Comprehensive Guide for Students
The surface area of a cylinder is a fundamental concept in geometry and mathematics, widely used in various real-world applications, such as architecture, engineering, and design. As a student, mastering the formula and calculations for cylinder surface area is crucial for problem-solving and critical thinking. In this worksheet, we will delve into the world of cylinders, explore the concept of surface area, and provide a step-by-step guide to help you become proficient in calculating the surface area of a cylinder.
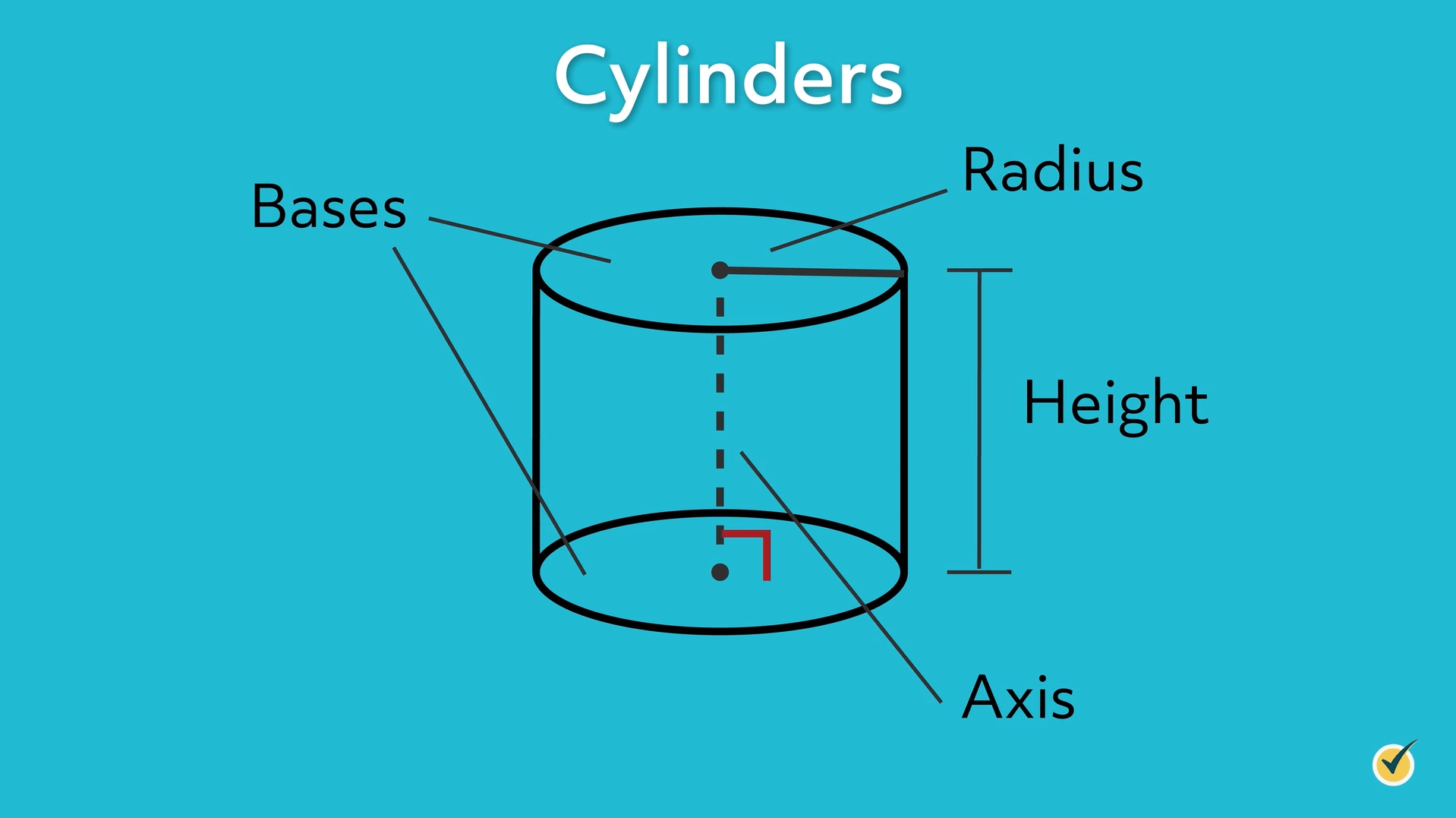
What is a Cylinder?
A cylinder is a three-dimensional shape with two parallel and circular bases connected by a curved lateral surface. It has two identical ends, which are circles, and a curved surface that wraps around the cylinder. The cylinder’s dimensions include its radius ®, height (h), and diameter (d).
Surface Area of a Cylinder Formula
The surface area of a cylinder (SA) can be calculated using the following formula:
SA = 2πr(h + r)
Where:
- π (pi) is a mathematical constant approximately equal to 3.14
- r is the radius of the cylinder
- h is the height of the cylinder
Breaking Down the Formula
Let’s break down the formula to understand its components:
- 2πr: This part of the formula calculates the area of the two circular bases.
- h: The height of the cylinder is used to calculate the area of the curved lateral surface.
- r: The radius is used again to calculate the area of the curved lateral surface.
Step-by-Step Guide to Calculating Cylinder Surface Area
Here’s a step-by-step guide to help you calculate the surface area of a cylinder:
- Find the radius ®: Identify the radius of the cylinder. Make sure it’s in the same units as the height (e.g., both in centimeters or meters).
- Find the height (h): Identify the height of the cylinder. Again, ensure it’s in the same units as the radius.
- Plug in the values: Substitute the values of radius ® and height (h) into the formula: SA = 2πr(h + r).
- Calculate the surface area: Perform the calculations to find the surface area of the cylinder.
Example Problems
Try solving these example problems to practice your skills:
| Cylinder | Radius ® | Height (h) | Surface Area (SA) |
|---|---|---|---|
| A | 4 cm | 10 cm | ? |
| B | 2 m | 5 m | ? |
| C | 6 cm | 8 cm | ? |
Use the formula SA = 2πr(h + r) to calculate the surface area of each cylinder.
📝 Note: Make sure to use the correct units for the radius and height, and to perform the calculations accurately.
Solving the Example Problems
Let’s solve the example problems:
| Cylinder | Radius ® | Height (h) | Surface Area (SA) |
|---|---|---|---|
| A | 4 cm | 10 cm | SA = 2π(4)(10 + 4) = 2π(4)(14) = 87.92 cm² |
| B | 2 m | 5 m | SA = 2π(2)(5 + 2) = 2π(2)(7) = 43.98 m² |
| C | 6 cm | 8 cm | SA = 2π(6)(8 + 6) = 2π(6)(14) = 263.76 cm² |
📝 Note: Round your answers to two decimal places for accuracy.
Real-World Applications
Understanding cylinder surface area has numerous real-world applications, such as:
- Architecture: Designing buildings, bridges, and other structures that involve cylindrical shapes.
- Engineering: Calculating the surface area of cylindrical components, like pipes and tubes.
- Design: Creating 3D models and prototypes that involve cylindrical shapes.
Conclusion
Mastering the concept of cylinder surface area is essential for students and professionals alike. With practice and patience, you can become proficient in calculating the surface area of cylinders using the formula SA = 2πr(h + r). Remember to apply the formula to real-world problems and explore its various applications in architecture, engineering, and design.
What is the formula for calculating the surface area of a cylinder?
+The formula for calculating the surface area of a cylinder is SA = 2πr(h + r), where π is a mathematical constant approximately equal to 3.14, r is the radius, and h is the height.
Why is understanding cylinder surface area important?
+Understanding cylinder surface area is crucial for problem-solving and critical thinking in various real-world applications, such as architecture, engineering, and design.
How can I practice calculating cylinder surface area?
+Practice calculating cylinder surface area by solving example problems, using online calculators or worksheets, and applying the formula to real-world problems.



