5 Ways to Master Supplementary Angles

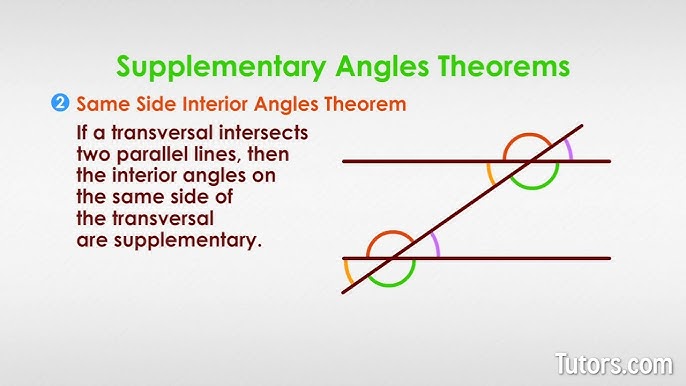
Understanding Supplementary Angles

When it comes to angles in geometry, there are several types that students need to be familiar with. One such type is supplementary angles. Supplementary angles are two angles whose measures add up to 180 degrees. In this article, we will explore five ways to master supplementary angles, including their definition, properties, and how to solve problems involving them.

1. Define and Identify Supplementary Angles

To master supplementary angles, it’s essential to understand their definition and how to identify them. Supplementary angles can be two acute angles, two obtuse angles, or a combination of an acute and an obtuse angle. When two angles are supplementary, they form a straight line.

📝 Note: Two angles are supplementary if the sum of their measures is 180 degrees.

For example, if we have two angles with measures 60 degrees and 120 degrees, they are supplementary because their sum is 180 degrees.

Example:

Angle A = 60 degrees Angle B = 120 degrees Sum of Angles A and B = 180 degrees

2. Use the Properties of Supplementary Angles

Supplementary angles have several properties that can be useful in solving problems. Here are a few:

• The sum of two supplementary angles is always 180 degrees.
• If two angles are supplementary, they are not necessarily adjacent or congruent.
• Supplementary angles can be used to find missing angles in a diagram.

📝 Note: Use the properties of supplementary angles to find missing angles in a diagram.

For example, if we have a diagram with two angles that form a straight line, we can use the property that the sum of supplementary angles is 180 degrees to find the missing angle.

Example:

Angle A = 60 degrees Angle B =? Sum of Angles A and B = 180 degrees

To find Angle B, we can subtract Angle A from 180 degrees:

Angle B = 180 - 60 = 120 degrees

3. Solve Problems Involving Supplementary Angles

Now that we have a good understanding of supplementary angles, let’s practice solving problems involving them. Here are a few examples:

• Find the measure of an angle that is supplementary to a given angle.
• Find the missing angle in a diagram using supplementary angles.
• Use supplementary angles to solve problems involving perimeter and area.

Example:

In a triangle, two angles have measures 30 degrees and 60 degrees. Find the measure of the third angle.

Since the sum of the angles in a triangle is 180 degrees, we can use supplementary angles to find the missing angle.

Angle A = 30 degrees Angle B = 60 degrees Angle C =?

Sum of Angles A, B, and C = 180 degrees

To find Angle C, we can subtract the sum of Angles A and B from 180 degrees:

Angle C = 180 - (30 + 60) = 90 degrees

4. Use Real-World Applications of Supplementary Angles

Supplementary angles have several real-world applications, including:

• Architecture: Supplementary angles are used in building design to ensure that walls and floors are straight and level.
• Engineering: Supplementary angles are used in bridge design to ensure that the bridge is stable and secure.
• Art: Supplementary angles are used in art to create symmetrical and balanced compositions.

📝 Note: Use real-world applications to make supplementary angles more interesting and relevant.

5. Practice, Practice, Practice!

Finally, to master supplementary angles, it’s essential to practice, practice, practice! Here are a few tips:

• Use online resources: There are many online resources available that provide practice problems and exercises on supplementary angles.
• Use worksheets: Worksheets are a great way to practice supplementary angles and can be found online or in math textbooks.
• Use real-world examples: Use real-world examples to make supplementary angles more interesting and relevant.

By following these five ways to master supplementary angles, students can gain a deeper understanding of this important concept in geometry.

As we wrap up this article, let’s summarize the key points:

• Supplementary angles are two angles whose measures add up to 180 degrees.
• Use the properties of supplementary angles to find missing angles in a diagram.
• Solve problems involving supplementary angles using real-world applications.
• Practice, practice, practice to master supplementary angles.

Related Terms:

• Supplementary angles worksheet PDF
• Supplementary angles Worksheet answer key
• Supplementary angles Worksheet Kuta
• Find missing angles worksheet pdf
• Math worksheet
• Vertical angles worksheet