5 Ways to Master Subtraction with Borrowing

Understanding Subtraction with Borrowing
Subtraction with borrowing is a fundamental concept in mathematics that can be challenging for some students to grasp. It involves subtracting a larger number from a smaller number, where the smaller number is not sufficient to subtract the larger number directly. In this case, we borrow from the next digit to facilitate the subtraction process. Mastering subtraction with borrowing requires practice, patience, and a clear understanding of the concept.
Method 1: Using the Standard Algorithm
The standard algorithm for subtraction with borrowing involves a step-by-step process:
- Start with the rightmost digit of the minuend (the number being subtracted from) and subtract the corresponding digit of the subtrahend (the number being subtracted).
- If the digit of the minuend is less than the digit of the subtrahend, borrow from the next digit to the left.
- Add 10 to the digit of the minuend and subtract the digit of the subtrahend.
- Repeat the process for each digit, moving from right to left.
📝 Note: When borrowing, make sure to decrease the digit from which you borrowed by 1.
Example:
| 4 | 5 | 2 |
| − | − | − |
| 2 | 7 | 1 |
- Start by subtracting 1 from 2, which gives us 1.
- Move to the next digit, 5. Since 5 is less than 7, we borrow from the next digit to the left, 4. We decrease 4 by 1 and add 10 to 5, making it 15.
- Now, we can subtract 7 from 15, which gives us 8.
- Finally, we subtract 2 from 3 (since we borrowed from 4), which gives us 1.
The final answer is 182.
Method 2: Using Visual Aids
Visual aids such as number lines, hundreds charts, and base-ten blocks can help students understand the concept of subtraction with borrowing.
- Number Lines: Create a number line with the minuend and subtrahend marked on it. Move the subtrahend to the left to represent the subtraction process. If the subtrahend is larger, move to the next number on the left and borrow from it.
- Hundreds Charts: Use hundreds charts to visualize the subtraction process. Highlight the minuend and subtrahend on the chart. If the subtrahend is larger, move to the next number on the left and borrow from it.
- Base-Ten Blocks: Use base-ten blocks to represent the minuend and subtrahend. If the subtrahend is larger, borrow from the next block to the left.
📝 Note: Visual aids can help students understand the concept of subtraction with borrowing, but they should also practice using the standard algorithm.
Method 3: Breaking Down Numbers
Breaking down numbers into hundreds, tens, and ones can help students understand the concept of subtraction with borrowing.
- Breaking Down the Minuend: Break down the minuend into hundreds, tens, and ones.
- Breaking Down the Subtrahend: Break down the subtrahend into hundreds, tens, and ones.
- Subtracting: Subtract the corresponding digits of the subtrahend from the minuend. If the subtrahend is larger, borrow from the next digit to the left.
Example:
| 4 | 5 | 2 |
| − | − | − |
| 2 | 7 | 1 |
- Break down the minuend into hundreds, tens, and ones: 400 + 50 + 2.
- Break down the subtrahend into hundreds, tens, and ones: 200 + 70 + 1.
- Subtract the corresponding digits: 400 - 200 = 200, 50 - 70 = -20 (borrow from 400), 2 - 1 = 1.
The final answer is 182.
Method 4: Using Real-World Examples
Using real-world examples can help students understand the concept of subtraction with borrowing.
- Shopping: Imagine you have 452 in your wallet and you spend 271 on shopping. How much money do you have left?
- Time: Imagine it is 4:52 PM and you have to wait for 2 hours and 71 minutes for a bus. What time will it be when the bus arrives?
Example:
| 4 | 5 | 2 |
| − | − | − |
| 2 | 7 | 1 |
- Imagine you have 452 and you spend 271. To find out how much money you have left, you need to subtract 271 from 452.
- Start by subtracting 1 from 2, which gives us 1.
- Move to the next digit, 5. Since 5 is less than 7, we borrow from the next digit to the left, 4. We decrease 4 by 1 and add 10 to 5, making it 15.
- Now, we can subtract 7 from 15, which gives us 8.
- Finally, we subtract 2 from 3 (since we borrowed from 4), which gives us 1.
The final answer is $182.
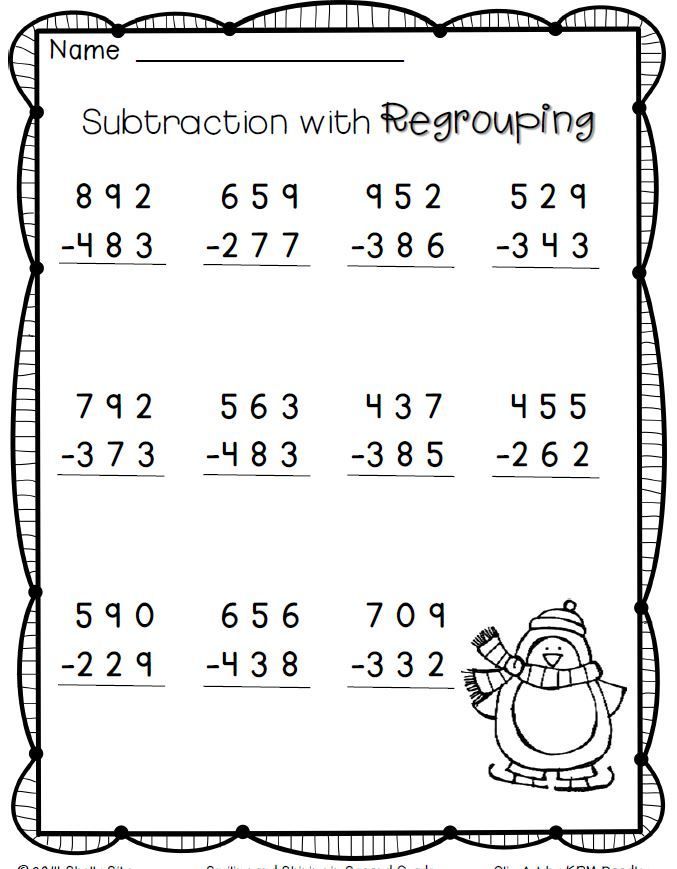
Method 5: Practicing with Worksheets
Practicing with worksheets can help students master subtraction with borrowing.
- Worksheets with Multiple-Digit Numbers: Practice subtracting multiple-digit numbers with borrowing.
- Worksheets with Word Problems: Practice solving word problems that involve subtraction with borrowing.
📝 Note: Practice regularly to build confidence and fluency in subtraction with borrowing.
In conclusion, mastering subtraction with borrowing requires practice, patience, and a clear understanding of the concept. By using the standard algorithm, visual aids, breaking down numbers, real-world examples, and practicing with worksheets, students can become proficient in subtraction with borrowing.
What is subtraction with borrowing?
+Subtraction with borrowing is a mathematical concept where a larger number is subtracted from a smaller number, requiring borrowing from the next digit to facilitate the subtraction process.
Why is subtraction with borrowing important?
+Subtraction with borrowing is an essential concept in mathematics, as it helps students understand the relationship between numbers and develop problem-solving skills.
How can I help my child master subtraction with borrowing?
+Encourage your child to practice regularly using worksheets, visual aids, and real-world examples. Also, provide feedback and guidance to help them build confidence and fluency in subtraction with borrowing.