5 Ways to Solve Piecewise Functions Easily
When it comes to solving piecewise functions, many students find themselves struggling to understand the concept and apply it to solve problems. However, with a few simple strategies and techniques, solving piecewise functions can become a breeze. In this article, we will explore five ways to solve piecewise functions easily.
What are Piecewise Functions?
Before we dive into the strategies, let’s first understand what piecewise functions are. A piecewise function is a function that is defined by multiple sub-functions, each applied to a specific interval of the domain. The sub-functions are “pieced together” to form the entire function.
5 Ways to Solve Piecewise Functions Easily
1. Identify the Intervals
The first step in solving piecewise functions is to identify the intervals on which each sub-function is defined. Look for the inequalities or equalities that define the intervals. For example, if we have a piecewise function defined as:
f(x) = { x^2, 0 ≤ x ≤ 2 2x + 1, x > 2 }
The intervals are [0, 2] and (2, ∞).
📝 Note: Make sure to identify the type of interval (closed or open) and the endpoints.
2. Evaluate Each Sub-Function
Once you have identified the intervals, evaluate each sub-function on its respective interval. For example, if we want to find the value of f(x) at x = 3, we would evaluate the sub-function 2x + 1, since 3 is in the interval (2, ∞).
3. Use a Number Line
A number line can be a useful tool in solving piecewise functions. Draw a number line and mark the endpoints of each interval. Then, evaluate each sub-function on its respective interval and mark the corresponding values on the number line.
| Interval | Sub-Function | Value |
|---|---|---|
| [0, 2] | x^2 | 4 |
| (2, ∞) | 2x + 1 | 7 |
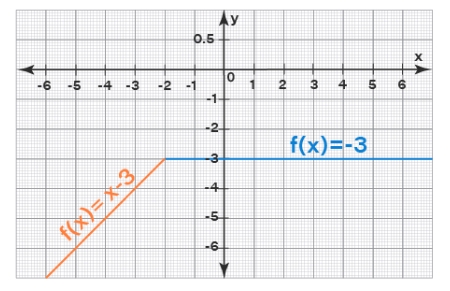
4. Graph the Piecewise Function
Graphing the piecewise function can also help you visualize the solution. Use a graphing calculator or software to graph each sub-function on its respective interval. Then, combine the graphs to form the entire piecewise function.
Example:
f(x) = { x^2, 0 ≤ x ≤ 2 2x + 1, x > 2 }
Graph of x^2 on [0, 2]:
Graph of 2x + 1 on (2, ∞):
Combine the graphs:
5. Use the Piecewise Function to Solve Equations
Finally, use the piecewise function to solve equations. For example, if we want to solve the equation f(x) = 5, we would evaluate each sub-function on its respective interval and find the values of x that satisfy the equation.
📝 Note: Make sure to check the solutions in the original equation to ensure they are valid.
By following these five strategies, you can easily solve piecewise functions and become more confident in your math skills.
Now that we have explored five ways to solve piecewise functions easily, let’s summarize the key points:
- Identify the intervals on which each sub-function is defined
- Evaluate each sub-function on its respective interval
- Use a number line to visualize the solution
- Graph the piecewise function to visualize the solution
- Use the piecewise function to solve equations
By mastering these strategies, you will be able to solve piecewise functions with ease and confidence.
What is a piecewise function?
+A piecewise function is a function that is defined by multiple sub-functions, each applied to a specific interval of the domain.
How do I identify the intervals of a piecewise function?
+Look for the inequalities or equalities that define the intervals. Make sure to identify the type of interval (closed or open) and the endpoints.
Can I use a graphing calculator to solve piecewise functions?
+Yes, a graphing calculator can be a useful tool in solving piecewise functions. You can graph each sub-function on its respective interval and combine the graphs to form the entire piecewise function.