Subtracting Fractions With Unlike Denominators Made Easy
Understanding Fractions with Unlike Denominators
Fractions are a fundamental concept in mathematics, and working with them can be challenging, especially when dealing with unlike denominators. Unlike denominators refer to fractions that have different denominators, making it difficult to perform arithmetic operations like addition and subtraction. However, with the right approach, subtracting fractions with unlike denominators can be made easy.
What Are Unlike Denominators?
Unlike denominators occur when two or more fractions have different numbers in the denominator. For example:
1⁄4 and 1⁄6 2⁄3 and 3⁄4 3⁄8 and 2⁄5
In each of these examples, the fractions have different denominators, making it challenging to perform arithmetic operations.
Why Do We Need to Find the Least Common Multiple (LCM)?
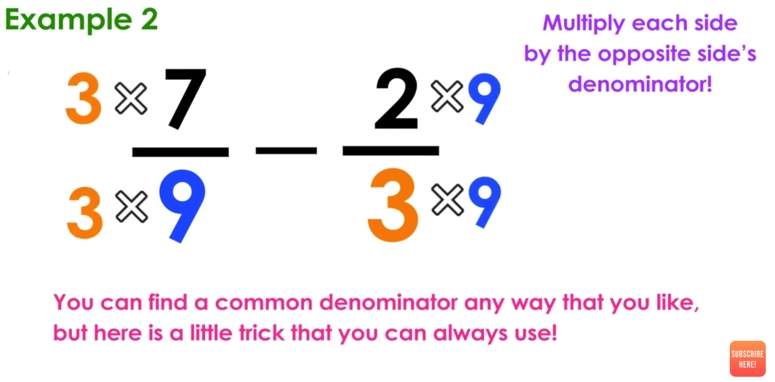
To subtract fractions with unlike denominators, we need to find the least common multiple (LCM) of the denominators. The LCM is the smallest number that both denominators can divide into evenly. Finding the LCM allows us to rewrite the fractions with like denominators, making it possible to subtract them.
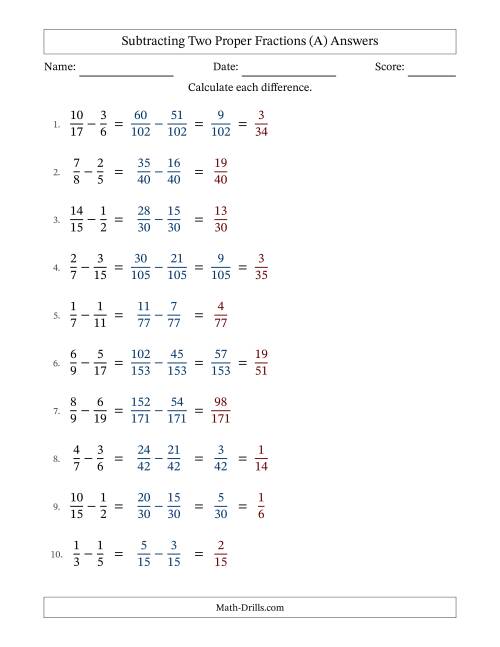
Step-by-Step Guide to Subtracting Fractions with Unlike Denominators
Here’s a step-by-step guide to subtracting fractions with unlike denominators:
- Identify the fractions: Write down the fractions you want to subtract. Make sure to identify the unlike denominators.
- Find the LCM: Find the least common multiple (LCM) of the denominators. You can use a list of multiples, prime factorization, or a calculator to find the LCM.
- Rewrite the fractions: Rewrite each fraction with the LCM as the new denominator. This will give you fractions with like denominators.
- Subtract the fractions: Subtract the fractions as you would with like denominators.
- Simplify the result: Simplify the result, if necessary.
📝 Note: Make sure to find the LCM of the denominators, not the numerators.
Example: Subtracting Fractions with Unlike Denominators
Let’s use the example:
1⁄4 - 1⁄6
Step 1: Identify the fractions We have two fractions: 1⁄4 and 1⁄6.
Step 2: Find the LCM The LCM of 4 and 6 is 12.
Step 3: Rewrite the fractions Rewrite each fraction with the LCM as the new denominator:
1⁄4 = 3⁄12 1⁄6 = 2⁄12
Step 4: Subtract the fractions Subtract the fractions:
3⁄12 - 2⁄12 = 1⁄12
Step 5: Simplify the result The result is already simplified.
Table: Finding the LCM of Common Denominators
| Denominators | LCM |
|---|---|
| 2, 3 | 6 |
| 4, 5 | 20 |
| 6, 8 | 24 |
| 9, 10 | 90 |
Tips and Tricks
- Use a list of multiples or prime factorization to find the LCM.
- Make sure to rewrite the fractions with the LCM as the new denominator.
- Simplify the result, if necessary.
- Practice, practice, practice! The more you practice, the easier it will become to subtract fractions with unlike denominators.
Mastery of Subtracting Fractions with Unlike Denominators
With practice and patience, you’ll become proficient in subtracting fractions with unlike denominators. Remember to find the LCM, rewrite the fractions, and simplify the result. By following these steps, you’ll be able to subtract fractions with unlike denominators with ease.
What is the least common multiple (LCM)?
+The least common multiple (LCM) is the smallest number that both denominators can divide into evenly.
How do I find the LCM of two denominators?
+You can use a list of multiples, prime factorization, or a calculator to find the LCM.
Can I subtract fractions with unlike denominators without finding the LCM?
+No, finding the LCM is necessary to rewrite the fractions with like denominators, making it possible to subtract them.