Mastering Special Triangles with Ease
Unlocking the Secrets of Special Triangles
Triangles are a fundamental concept in geometry, and special triangles are a crucial part of it. Mastering special triangles can make a significant difference in solving complex geometric problems with ease. In this article, we will delve into the world of special triangles, exploring their properties, types, and applications.
Understanding the Basics of Triangles
Before diving into special triangles, it’s essential to understand the basics of triangles. A triangle is a polygon with three sides and three angles. The sum of the interior angles of a triangle is always 180 degrees. Triangles can be classified based on their angles and sides.
Types of Triangles
- Acute Triangle: A triangle with all acute angles (less than 90 degrees).
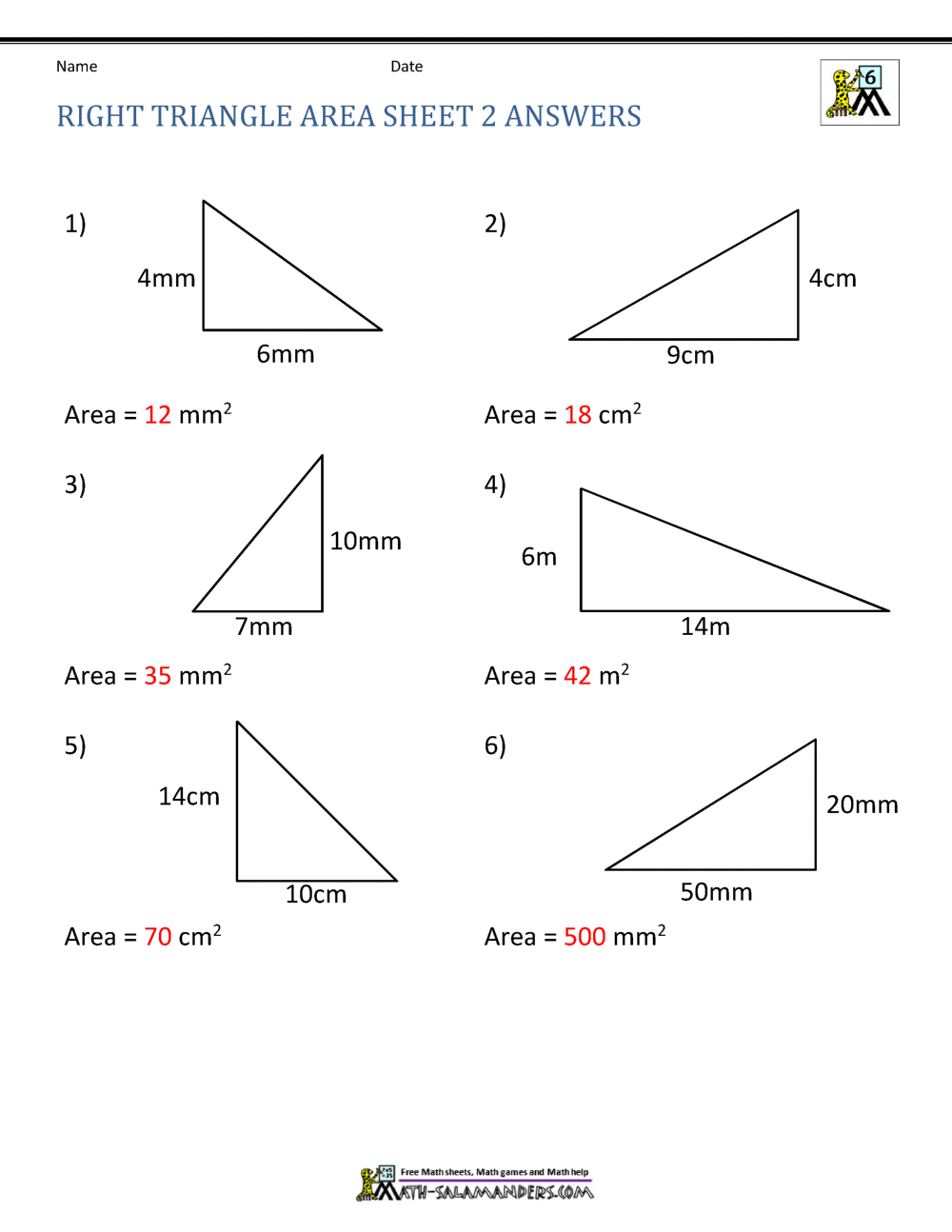
- Right Triangle: A triangle with one right angle (exactly 90 degrees).
- Obtuse Triangle: A triangle with one obtuse angle (greater than 90 degrees).
- Equilateral Triangle: A triangle with all sides of equal length.
- Isosceles Triangle: A triangle with two sides of equal length.
- Scalene Triangle: A triangle with all sides of different lengths.
Special Triangles: Properties and Applications
Special triangles are triangles with unique properties that make them useful in various mathematical and real-world applications. Here are some of the most common special triangles:
1. 45-45-90 Triangle
A 45-45-90 triangle is a right triangle with two 45-degree angles. The side opposite the right angle is the hypotenuse, and the other two sides are congruent.
- Properties: The ratio of the sides is 1:1:√2.
- Applications: 45-45-90 triangles are commonly used in architecture, engineering, and design.
2. 30-60-90 Triangle
A 30-60-90 triangle is a right triangle with one 30-degree angle and one 60-degree angle. The side opposite the 30-degree angle is half the length of the hypotenuse, and the side opposite the 60-degree angle is √3 times the length of the side opposite the 30-degree angle.
- Properties: The ratio of the sides is 1:√3:2.
- Applications: 30-60-90 triangles are often used in trigonometry, physics, and engineering.
3. Equilateral Triangle
An equilateral triangle is a triangle with all sides of equal length. Each angle of an equilateral triangle is 60 degrees.
- Properties: All sides are equal, and all angles are 60 degrees.
- Applications: Equilateral triangles are commonly used in art, design, and architecture.
4. Isosceles Triangle
An isosceles triangle is a triangle with two sides of equal length. The angles opposite the equal sides are also equal.
- Properties: Two sides are equal, and the base angles are equal.
- Applications: Isosceles triangles are often used in engineering, architecture, and physics.
Real-World Applications of Special Triangles
Special triangles have numerous real-world applications in various fields, including:
- Architecture: Special triangles are used in designing buildings, bridges, and other structures.
- Engineering: Special triangles are used in designing electronic circuits, mechanical systems, and other engineering applications.
- Physics: Special triangles are used in describing the motion of objects, forces, and energies.
- Art and Design: Special triangles are used in creating visually appealing compositions and designs.
Conclusion
Mastering special triangles can make a significant difference in solving complex geometric problems with ease. By understanding the properties and applications of special triangles, you can unlock new possibilities in various fields. Remember, practice makes perfect, so keep practicing and exploring the world of special triangles!
What is the difference between a 45-45-90 triangle and a 30-60-90 triangle?
+A 45-45-90 triangle has two 45-degree angles, while a 30-60-90 triangle has one 30-degree angle and one 60-degree angle.
What is the ratio of the sides in a 30-60-90 triangle?
+The ratio of the sides in a 30-60-90 triangle is 1:√3:2.
What is an example of a real-world application of special triangles?
+Special triangles are used in designing electronic circuits, mechanical systems, and other engineering applications.
Related Terms:
- Special Right Triangles answer Key
- Special right triangles Notes
- 30-60-90 triangle worksheet
- special right triangles worksheet 45-45-90
- Special right triangles formula



