Solving Two-Step Inequalities Made Easy

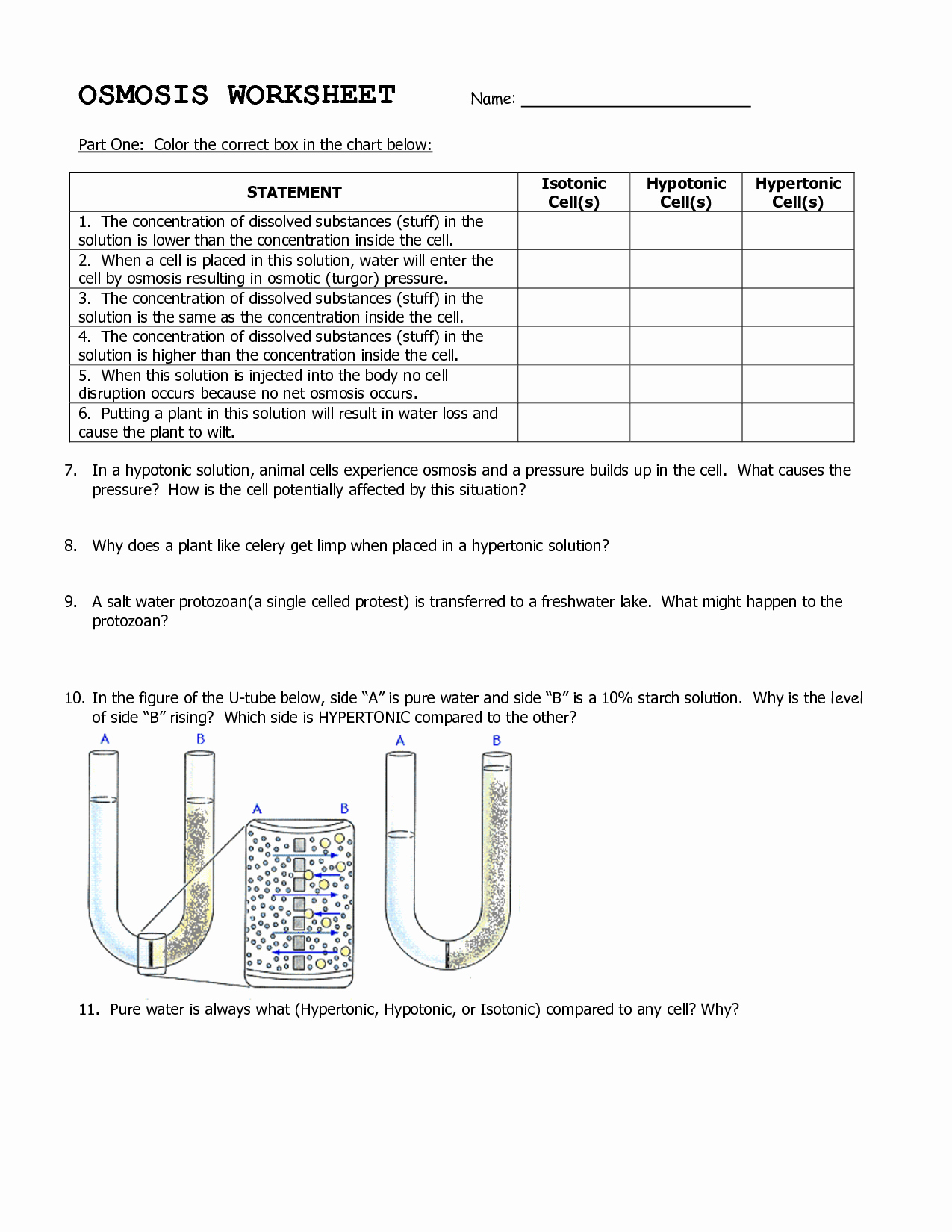
Understanding Two-Step Inequalities
When it comes to solving inequalities, two-step inequalities can be a bit more challenging than one-step inequalities. However, with the right approach, you can easily solve them. In this post, we’ll take a step-by-step approach to solving two-step inequalities and provide you with some valuable tips and tricks to make the process easier.
What are Two-Step Inequalities?
A two-step inequality is an inequality that requires two operations to solve. It involves adding or subtracting a number and then multiplying or dividing by another number. Two-step inequalities can be represented in the following forms:
- ax + b > c
- ax + b < c
- ax - b > c
- ax - b < c
where a, b, and c are constants, and x is the variable.
Step-by-Step Guide to Solving Two-Step Inequalities
To solve a two-step inequality, you need to follow these steps:
- Isolate the variable: The first step is to isolate the variable by adding or subtracting the constant term to both sides of the inequality. This will help you get rid of the constant term and make it easier to solve for the variable.
- Multiply or divide both sides: Once you’ve isolated the variable, you need to multiply or divide both sides of the inequality by the coefficient of the variable. This will help you solve for the variable.
- Check the direction of the inequality: When multiplying or dividing both sides of the inequality, you need to be careful about the direction of the inequality. If you multiply or divide both sides by a negative number, you need to reverse the direction of the inequality.
🤔 Note: When solving two-step inequalities, it's essential to keep track of the direction of the inequality. If you're unsure, try plugging in a test value to check the direction.
Example 1: Solving a Two-Step Inequality
Let’s solve the inequality 2x + 5 > 11.
- Isolate the variable: Subtract 5 from both sides of the inequality to get 2x > 6.
- Multiply both sides: Divide both sides by 2 to get x > 3.
The solution to the inequality is x > 3.
Example 2: Solving a Two-Step Inequality
Let’s solve the inequality x - 3 < 7.
- Isolate the variable: Add 3 to both sides of the inequality to get x < 10.
- Multiply both sides: No multiplication is required in this case, as the coefficient of x is 1.
The solution to the inequality is x < 10.
Tips and Tricks for Solving Two-Step Inequalities
- Use inverse operations: When solving two-step inequalities, use inverse operations to isolate the variable. For example, if you have 2x + 5, you can subtract 5 from both sides and then divide both sides by 2.
- Check the direction of the inequality: Always check the direction of the inequality when multiplying or dividing both sides. If you multiply or divide both sides by a negative number, reverse the direction of the inequality.
- Use a number line: Visualizing the inequality on a number line can help you understand the solution set and check your answer.

| Inequality | Solution |
|---|---|
| 2x + 5 > 11 | x > 3 |
| x - 3 < 7 | x < 10 |
Common Mistakes to Avoid
- Forgetting to check the direction of the inequality: Always check the direction of the inequality when multiplying or dividing both sides.
- Not isolating the variable: Make sure to isolate the variable by adding or subtracting the constant term to both sides of the inequality.
- Not using inverse operations: Use inverse operations to isolate the variable and solve for the variable.
In summary, solving two-step inequalities requires isolating the variable, multiplying or dividing both sides, and checking the direction of the inequality. By following these steps and using inverse operations, you can easily solve two-step inequalities.
Solving two-step inequalities is a fundamental concept in algebra, and with practice, you’ll become more comfortable and confident in your ability to solve them. Remember to always check your work and use a number line to visualize the solution set.
What is a two-step inequality?
+A two-step inequality is an inequality that requires two operations to solve. It involves adding or subtracting a number and then multiplying or dividing by another number.
How do I solve a two-step inequality?
+To solve a two-step inequality, you need to isolate the variable by adding or subtracting the constant term to both sides, and then multiply or divide both sides by the coefficient of the variable.
What is the most common mistake when solving two-step inequalities?
+The most common mistake is forgetting to check the direction of the inequality when multiplying or dividing both sides.
Related Terms:
- Solving Inequalities Worksheet PDF
- two-step inequalities worksheet 7th grade
- Solving one-Step Inequalities Worksheet PDF