Solve Systems of Equations Easily with Graphing Techniques
Understanding the Basics of Graphing Techniques
Graphing techniques are a powerful tool for solving systems of equations. By visualizing the equations as lines or curves on a graph, you can easily identify the solution to the system. In this article, we will explore the basics of graphing techniques and how to use them to solve systems of equations.
📝 Note: It's essential to have a basic understanding of algebra and graphing concepts before diving into this topic.
What is a System of Equations?
A system of equations is a set of two or more equations that contain the same variables. These equations can be linear or nonlinear, and they can be represented graphically using lines or curves. The goal of solving a system of equations is to find the values of the variables that satisfy all the equations in the system.
Types of Systems of Equations
There are several types of systems of equations, including:
- Linear systems: These are systems of linear equations, where each equation can be represented as a straight line on a graph.
- Nonlinear systems: These are systems of nonlinear equations, where each equation can be represented as a curve on a graph.
- Consistent systems: These are systems of equations that have a solution, meaning that there is at least one point that satisfies all the equations in the system.
- Inconsistent systems: These are systems of equations that do not have a solution, meaning that there is no point that satisfies all the equations in the system.
Graphing Techniques for Solving Systems of Equations
Graphing techniques are a powerful tool for solving systems of equations. By visualizing the equations as lines or curves on a graph, you can easily identify the solution to the system. Here are some common graphing techniques used to solve systems of equations:
- Graphing by Plotting Points: This method involves plotting points on a graph to visualize the equations. By plotting points, you can identify the solution to the system by finding the point of intersection between the lines or curves.
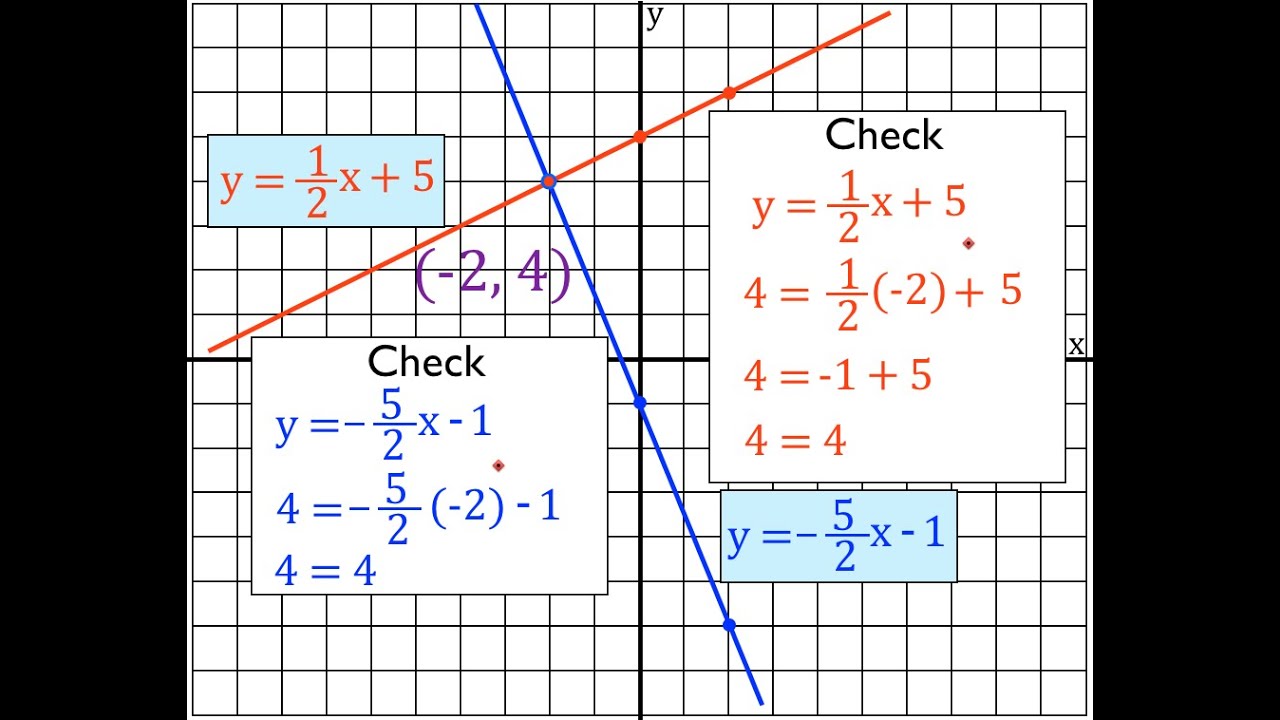
- Graphing using Slope-Intercept Form: This method involves rewriting the equations in slope-intercept form (y = mx + b) and graphing them on a slope-intercept graph. By finding the point of intersection between the lines, you can identify the solution to the system.
- Graphing using Standard Form: This method involves rewriting the equations in standard form (Ax + By = C) and graphing them on a standard graph. By finding the point of intersection between the lines, you can identify the solution to the system.
Example: Solving a Linear System using Graphing Techniques
Suppose we have the following linear system:
x + y = 4 x - y = 2
To solve this system using graphing techniques, we can graph the two equations on a coordinate plane.
| x | y |
|---|---|
| 0 | 4 |
| 2 | 2 |
| 4 | 0 |
By plotting points and drawing the lines, we can see that the point of intersection between the two lines is (2, 2). Therefore, the solution to the system is x = 2 and y = 2.
Tips and Tricks for Using Graphing Techniques
Here are some tips and tricks for using graphing techniques to solve systems of equations:
- Use a Graphing Calculator: A graphing calculator can be a powerful tool for solving systems of equations. It can help you graph the equations quickly and easily, and it can also help you find the solution to the system.
- Check for Consistency: Before solving a system of equations, make sure to check for consistency. If the system is inconsistent, there is no solution, and you can save yourself time by not attempting to solve it.
- Use Different Colors: When graphing multiple equations, use different colors to distinguish between them. This can help you visualize the equations more clearly and make it easier to find the solution.
Common Mistakes to Avoid
Here are some common mistakes to avoid when using graphing techniques to solve systems of equations:
- Not Checking for Consistency: Failing to check for consistency can lead to wasting time trying to solve an inconsistent system.
- Not Using a Graphing Calculator: Not using a graphing calculator can make it more difficult to graph the equations and find the solution.
- Not Using Different Colors: Not using different colors can make it more difficult to distinguish between the equations and find the solution.
When solving systems of equations, it’s essential to use a combination of algebraic and graphical methods. By using graphing techniques, you can visualize the equations and find the solution more easily.
What is the difference between a consistent and inconsistent system of equations?
+A consistent system of equations has a solution, meaning that there is at least one point that satisfies all the equations in the system. An inconsistent system of equations does not have a solution, meaning that there is no point that satisfies all the equations in the system.
What are some common graphing techniques used to solve systems of equations?
+Some common graphing techniques used to solve systems of equations include graphing by plotting points, graphing using slope-intercept form, and graphing using standard form.
What are some tips and tricks for using graphing techniques to solve systems of equations?
+Some tips and tricks for using graphing techniques to solve systems of equations include using a graphing calculator, checking for consistency, and using different colors to distinguish between the equations.



