5 Ways to Find the Volume of a Sphere

Understanding the Basics of a Sphere's Volume
When dealing with three-dimensional shapes, calculating their volumes can be an essential task in various fields such as mathematics, physics, and engineering. A sphere, being one of the simplest yet most fascinating shapes, has a volume that can be calculated using a few straightforward methods. This article will delve into five ways to find the volume of a sphere, exploring both traditional and innovative approaches.
Method 1: Using the Standard Formula
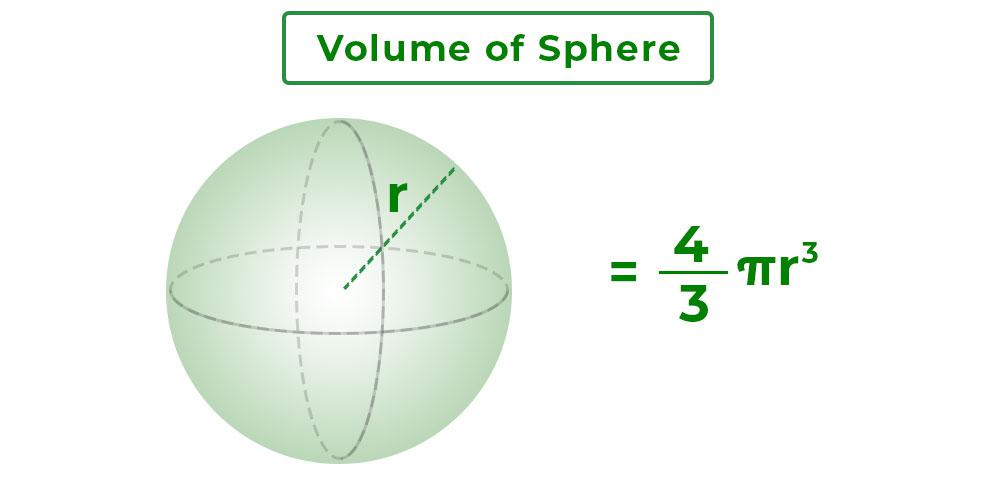
The most common method to calculate the volume of a sphere is by using the standard formula:
V = (4⁄3) * π * r^3
Where: - V is the volume of the sphere - π (pi) is a mathematical constant approximately equal to 3.14159 - r is the radius of the sphere
This formula is widely accepted and used across different disciplines. However, for those interested in the derivation of this formula, it involves integrating the area of a circle (πr^2) with respect to the radius.
📝 Note: This method assumes you have the radius of the sphere. If you only have the diameter, simply divide it by 2 to obtain the radius.
Method 2: Using the Diameter
While the radius is a more natural parameter for the standard formula, sometimes you might only have the diameter. To calculate the volume using the diameter, you can first find the radius (as mentioned in the note above) and then apply the standard formula. Alternatively, you can directly use a formula that incorporates the diameter:
V = (1⁄6) * π * d^3
Where: - V is the volume of the sphere - π (pi) is a mathematical constant approximately equal to 3.14159 - d is the diameter of the sphere
This formula is derived by substituting the radius with the diameter divided by 2 in the standard formula.
Method 3: Using the Circumference
If you know the circumference of the sphere’s great circle (which is any circle that divides the sphere into two equal hemispheres), you can calculate the volume. The formula for the circumference is:
C = 2 * π * r
Given the circumference, you can rearrange this formula to find the radius:
r = C / (2 * π)
Once you have the radius, you can use the standard volume formula to find the volume.
Method 4: Using the Surface Area
The surface area (A) of a sphere is given by:
A = 4 * π * r^2
If you know the surface area, you can find the radius by rearranging this formula:
r = √(A / (4 * π))
With the radius known, you can again use the standard volume formula to calculate the volume.
Method 5: Approximation Using a Cylinder
For a more visual or practical approach, you can approximate the volume of a sphere by inscribing it within a cylinder. The sphere will touch the sides of the cylinder, and its diameter will be equal to the height of the cylinder. The volume of the cylinder is:
V_cylinder = π * r^2 * h
Since the diameter of the sphere equals the height of the cylinder:
h = d = 2r
Substituting this into the cylinder volume formula gives:
V_cylinder = π * r^2 * 2r = 2 * π * r^3
The actual volume of the sphere is slightly less than this due to the empty spaces around the sphere within the cylinder. However, for a rough estimation or for educational purposes, this method can provide an intuitive understanding of the sphere’s volume.
Summary of Volume Formulas
| Method | Formula |
|---|---|
| Standard | V = (4⁄3) * π * r^3 |
| Diameter | V = (1⁄6) * π * d^3 |
| Circumference | V = (4⁄3) * π * (C / (2 * π))^3 |
| Surface Area | V = (4⁄3) * π * (√(A / (4 * π)))^3 |
| Cylinder Approximation | V ≈ 2 * π * r^3 |
In conclusion, the volume of a sphere can be calculated using various methods, each with its own advantages depending on the information available. Understanding these different approaches can help deepen one’s comprehension of geometric shapes and their properties.
What is the most accurate method to calculate the volume of a sphere?
+The most accurate method is using the standard formula V = (4⁄3) * π * r^3, given that you have the precise value of the radius.
Can I calculate the volume of a sphere without knowing the radius or diameter?
+Yes, you can use the surface area or the circumference to find the radius and then calculate the volume.
What is the purpose of using the cylinder approximation method?
+The cylinder approximation method provides a rough estimation and is useful for educational purposes or when precise calculations are not necessary.
Related Terms:
- Surface area of sphere Worksheet
- Volume of cylinder Worksheet PDF
- Volume of cone Worksheet