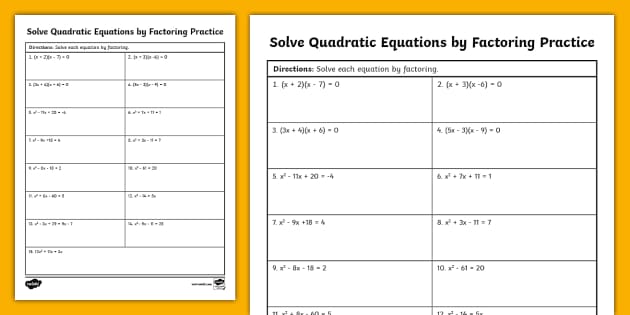
5 Ways to Solve Quadratic Equations by Factoring

Understanding Quadratic Equations

Quadratic equations are a fundamental concept in algebra, and they have numerous applications in various fields, including physics, engineering, and computer science. A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable (usually x) is two. The general form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants, and a cannot be zero.

The Importance of Factoring

Factoring is a crucial technique in solving quadratic equations. It involves expressing the quadratic equation as a product of two binomial expressions. Factoring can help you solve quadratic equations quickly and efficiently, especially when the equations have integer roots. In this article, we will discuss five ways to solve quadratic equations by factoring.

Method 1: Factoring by Finding Two Numbers

This method involves finding two numbers whose product is equal to the constant term © and whose sum is equal to the coefficient of the linear term (b). For example, consider the quadratic equation x^2 + 5x + 6 = 0. To factor this equation, we need to find two numbers whose product is 6 and whose sum is 5. The numbers are 2 and 3, since 2 × 3 = 6 and 2 + 3 = 5. Therefore, we can write the equation as (x + 2)(x + 3) = 0.

Method 2: Factoring by Grouping

This method involves grouping the terms of the quadratic equation in a way that allows us to factor out a common binomial expression. For example, consider the quadratic equation x^2 + 4x + 4 = 0. We can group the terms as (x^2 + 4x) + 4 = 0. Then, we can factor out a common binomial expression: x(x + 4) + 4 = 0. Finally, we can write the equation as (x + 2)(x + 2) = 0.

Method 3: Factoring by Using the AC Method

This method involves using the product of the coefficients of the quadratic term (a) and the constant term © to factor the equation. For example, consider the quadratic equation x^2 + 6x + 8 = 0. The product of the coefficients is ac = 1 × 8 = 8. We need to find two numbers whose product is 8 and whose sum is 6. The numbers are 2 and 4, since 2 × 4 = 8 and 2 + 4 = 6. Therefore, we can write the equation as (x + 2)(x + 4) = 0.

Method 4: Factoring by Using the CO Method

This method involves using the sum and product of the coefficients of the linear term (b) and the constant term © to factor the equation. For example, consider the quadratic equation x^2 + 7x + 12 = 0. The sum of the coefficients is b + c = 7 + 12 = 19. We need to find two numbers whose product is 12 and whose sum is 7. The numbers are 3 and 4, since 3 × 4 = 12 and 3 + 4 = 7. Therefore, we can write the equation as (x + 3)(x + 4) = 0.

Method 5: Factoring by Using the Diamond Method

This method involves using a diamond-shaped diagram to factor the quadratic equation. For example, consider the quadratic equation x^2 + 9x + 20 = 0. We can create a diamond-shaped diagram with the coefficients:

a	b	c
1	9	20

We can then use the diagram to find the factors of the quadratic equation. The factors are (x + 4)(x + 5) = 0.

📝 Note: The diamond method is a visual tool that can help you factor quadratic equations quickly and efficiently.

In conclusion, there are five ways to solve quadratic equations by factoring: finding two numbers, factoring by grouping, using the AC method, using the CO method, and using the diamond method. Each method has its own strengths and weaknesses, and the choice of method depends on the specific quadratic equation being solved.