5 Ways to Solve Equations Easily
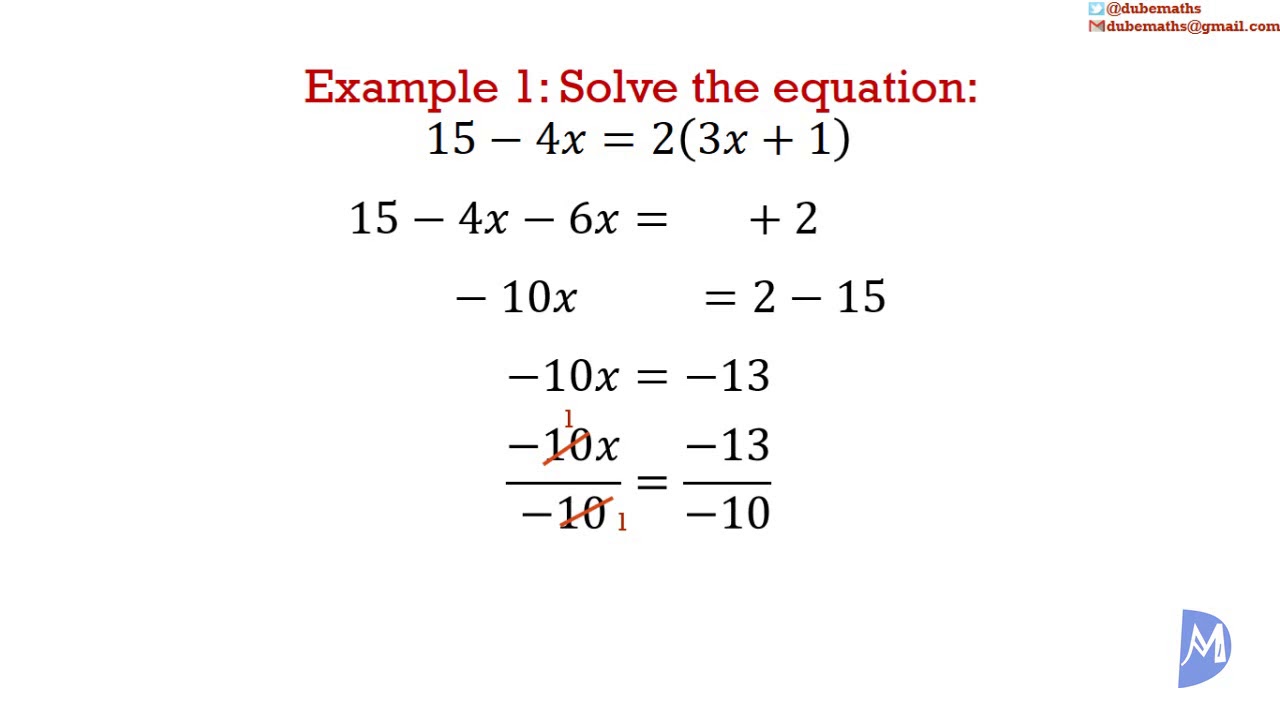
Understanding the Basics of Equations
Equations are a fundamental part of mathematics, and being able to solve them is crucial for various fields, including science, engineering, economics, and more. An equation is a statement that expresses the equality of two mathematical expressions, often containing variables. Solving an equation means finding the value of the variable that makes the equation true. In this blog post, we will explore five ways to solve equations easily, starting with the basics and moving on to more advanced techniques.
1. Simplifying Equations
Before diving into solving equations, it’s essential to simplify them as much as possible. This involves combining like terms, removing parentheses, and rearranging the equation to make it more manageable.
Example:
Simplify the equation: 2x + 5 + 3x - 2 = 11
Solution:
Combine like terms: 2x + 3x = 5x Remove constants: 5x + 5 - 2 = 11 Combine constants: 5x + 3 = 11
Simplified Equation: 5x + 3 = 11
📝 Note: Simplifying equations can help reduce the complexity of the problem and make it easier to solve.
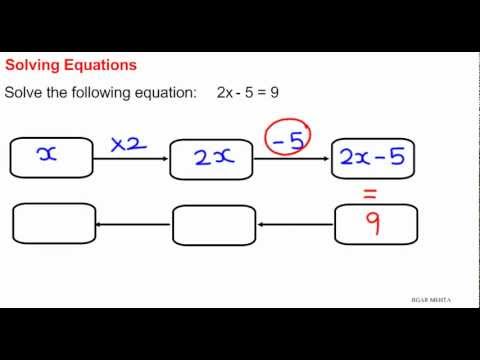
2. Using Inverse Operations
Inverse operations are a straightforward way to solve equations. This method involves using the opposite operation to isolate the variable.
Example:
Solve the equation: 2x = 12
Solution:
Divide both sides by 2: x = 12 ÷ 2 x = 6
Example:
Solve the equation: x - 3 = 7
Solution:
Add 3 to both sides: x = 7 + 3 x = 10
Inverse Operations Table:
| Operation | Inverse Operation |
|---|---|
| Addition (+) | Subtraction (-) |
| Subtraction (-) | Addition (+) |
| Multiplication (×) | Division (÷) |
| Division (÷) | Multiplication (×) |
3. Using Distributive Property
The distributive property is a useful technique for solving equations involving parentheses.
Example:
Solve the equation: 2(x + 3) = 12
Solution:
Distribute the 2: 2x + 6 = 12 Subtract 6 from both sides: 2x = 6 Divide both sides by 2: x = 6 ÷ 2 x = 3
Example:
Solve the equation: x/2 + 3 = 7
Solution:
Subtract 3 from both sides: x/2 = 4 Multiply both sides by 2: x = 8
4. Using Linear Equations
Linear equations are equations in which the highest power of the variable is 1. These equations can be solved using the slope-intercept form (y = mx + b).
Example:
Solve the equation: 2x - 3y = 7
Solution:
Rearrange the equation to slope-intercept form: y = (2⁄3)x - 7⁄3
Example:
Solve the equation: x + 2y = 5
Solution:
Rearrange the equation to slope-intercept form: y = (-1⁄2)x + 5⁄2
5. Using Quadratic Equations
Quadratic equations are equations in which the highest power of the variable is 2. These equations can be solved using the quadratic formula (x = (-b ± √(b² - 4ac)) / 2a).
Example:
Solve the equation: x² + 5x + 6 = 0
Solution:
Use the quadratic formula: x = (-5 ± √(5² - 4(1)(6))) / 2(1) x = (-5 ± √(25 - 24)) / 2 x = (-5 ± √1) / 2 x = (-5 ± 1) / 2 x = -2 or x = -3
In conclusion, solving equations can be a challenging task, but with the right techniques, it can become much easier. By simplifying equations, using inverse operations, distributive property, linear equations, and quadratic equations, you can solve a wide range of equations with confidence.
What is the difference between a linear and quadratic equation?
+A linear equation is an equation in which the highest power of the variable is 1, whereas a quadratic equation is an equation in which the highest power of the variable is 2.
How do I simplify an equation?
+To simplify an equation, combine like terms, remove parentheses, and rearrange the equation to make it more manageable.
What is the quadratic formula?
+The quadratic formula is a formula used to solve quadratic equations, which is x = (-b ± √(b² - 4ac)) / 2a.
Related Terms:
- Solving equations grade 8 Worksheet
- Math worksheet
- Algebraic expression Worksheet PDF
- Worksheet Math grade 3