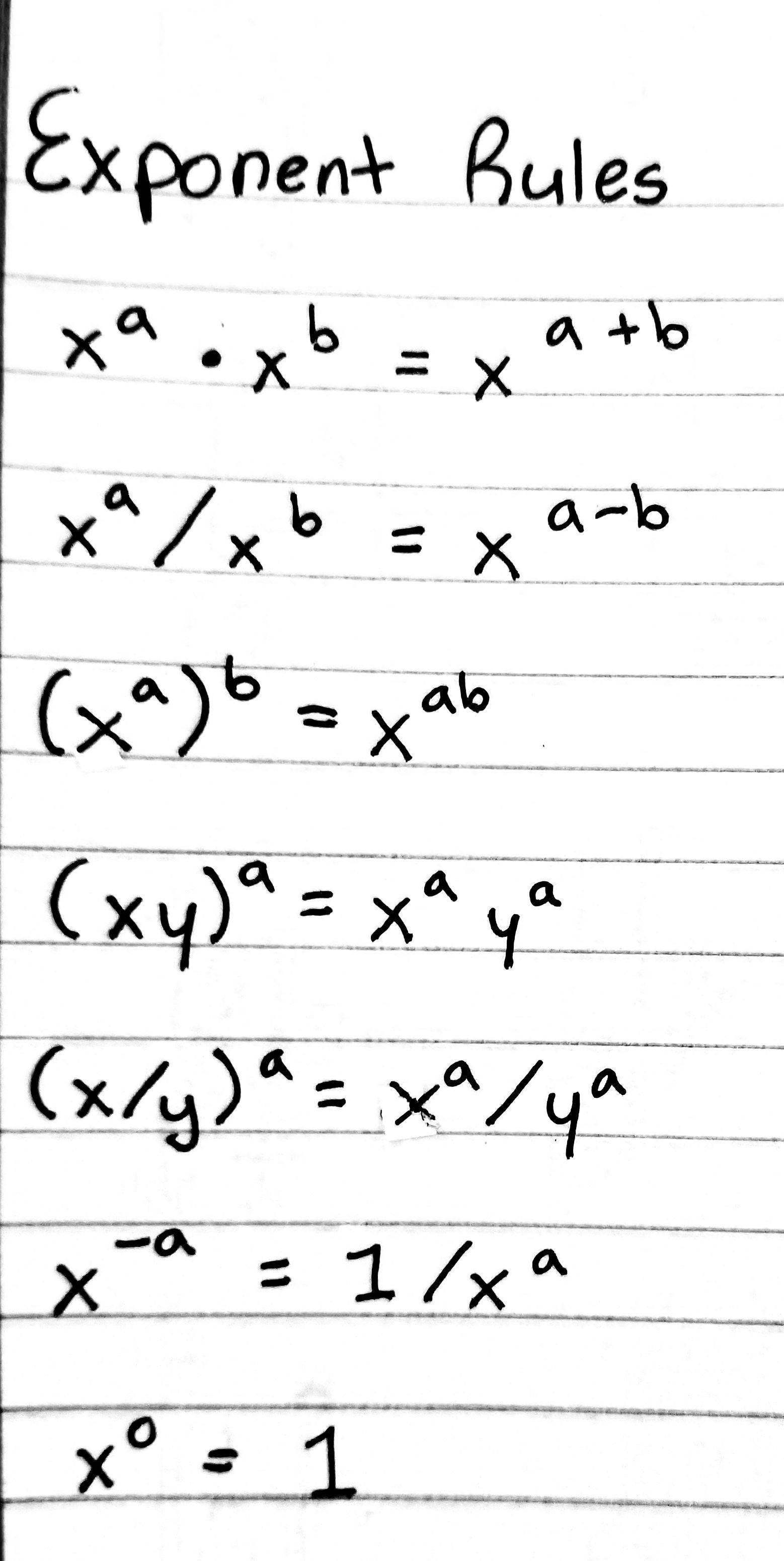5 Ways to Clear Fractions in Equations

When dealing with fractions in equations, it’s often necessary to clear them to simplify the equation and solve for the variable. Clearing fractions can be a bit tricky, but don’t worry, we’ve got you covered. In this article, we’ll explore five ways to clear fractions in equations, along with examples and explanations to help you master this essential algebra skill.

h2>Method 1: Multiplying Both Sides by the LCD

One of the most common methods for clearing fractions is to multiply both sides of the equation by the least common denominator (LCD) of the fractions. This method works because the LCD is the smallest number that all the denominators can divide into evenly.

For example, let’s say we have the equation:

2/3x + ¹⁄₄ = ³⁄₄

To clear the fractions, we need to find the LCD of the denominators, which is 12. We can then multiply both sides of the equation by 12 to get:

8x + 3 = 9

Now we can solve for x by subtracting 3 from both sides and then dividing both sides by 8:

8x = 6

x = ⁶⁄₈

x = ³⁄₄

p class=“pro-note”>📝 Note: When multiplying both sides by the LCD, make sure to multiply all terms in the equation, including the constant terms.

h2>Method 2: Using the “Flip and Multiply” Method

Another way to clear fractions is to use the “flip and multiply” method. This method involves flipping the fraction on the right-hand side of the equation and then multiplying both sides by the flipped fraction.

For example, let’s say we have the equation:

2/3x = ³⁄₄

To clear the fraction, we can flip the fraction on the right-hand side and then multiply both sides by the flipped fraction:

2/3x = ³⁄₄

Multiply both sides by ⁴⁄₃:

2x = 3

Now we can solve for x by dividing both sides by 2:

x = ³⁄₂

p class=“pro-note”>📝 Note: The “flip and multiply” method only works when there is a single fraction on the right-hand side of the equation.

h2>Method 3: Using a Common Denominator

When there are multiple fractions in an equation, we can use a common denominator to clear them. This method involves finding the least common multiple (LCM) of the denominators and then converting each fraction to have the LCM as the denominator.

For example, let’s say we have the equation:

1/2x + ¹⁄₄ = ³⁄₄

To clear the fractions, we can find the LCM of the denominators, which is 4. We can then convert each fraction to have a denominator of 4:

2/4x + ¹⁄₄ = ³⁄₄

Now we can add the fractions on the left-hand side:

3/4x = ³⁄₄

Next, we can multiply both sides by 4 to clear the fraction:

3x = 3

Now we can solve for x by dividing both sides by 3:

x = 1

p class=“pro-note”>📝 Note: When using a common denominator, make sure to convert all fractions to have the same denominator.

h2>Method 4: Using a Multiplication Property

Another way to clear fractions is to use a multiplication property. This method involves multiplying both sides of the equation by a number that will eliminate the fraction.

For example, let’s say we have the equation:

2/3x = 2

To clear the fraction, we can multiply both sides by 3:

2x = 6

Now we can solve for x by dividing both sides by 2:

x = 3

p class=“pro-note”>📝 Note: The multiplication property method only works when there is a single fraction on the left-hand side of the equation.

h2>Method 5: Using a Division Property

Finally, we can use a division property to clear fractions. This method involves dividing both sides of the equation by a number that will eliminate the fraction.

For example, let’s say we have the equation:

2x = ²⁄₃

To clear the fraction, we can divide both sides by 2:

x = ¹⁄₃

Now we can solve for x by multiplying both sides by 3:

x = 1

p class=“pro-note”>📝 Note: The division property method only works when there is a single fraction on the right-hand side of the equation.

Clearing fractions in equations is an essential algebra skill that can be mastered with practice and patience. By using one of the five methods outlined above, you can simplify equations and solve for the variable with ease. Remember to always check your work and use the method that works best for the given equation.

**table>

Method
Example
Notes


Multiplying Both Sides by the LCD
2/3x + ¹⁄₄ = ³⁄₄
Find the LCD and multiply both sides


Using the “Flip and Multiply” Method
2/3x = ³⁄₄
Flip the fraction and multiply both sides


Using a Common Denominator
1/2x + ¹⁄₄ = ³⁄₄
Find the LCM and convert each fraction


Using a Multiplication Property
2/3x = 2
Multiply both sides by a number to eliminate the fraction


Using a Division Property
2x = ²⁄₃
Divide both sides by a number to eliminate the fraction