5 Ways to Find Slope from a Graph
Understanding Slope and Its Importance in Graphs
In mathematics, the slope of a line is a measure of how much it rises (or falls) vertically over a given horizontal distance. It’s a fundamental concept in algebra and geometry, and finding the slope from a graph is a crucial skill for problem-solving and critical thinking. The slope can be calculated using the graph of a line, and there are several methods to do so. In this article, we will explore five ways to find the slope from a graph.
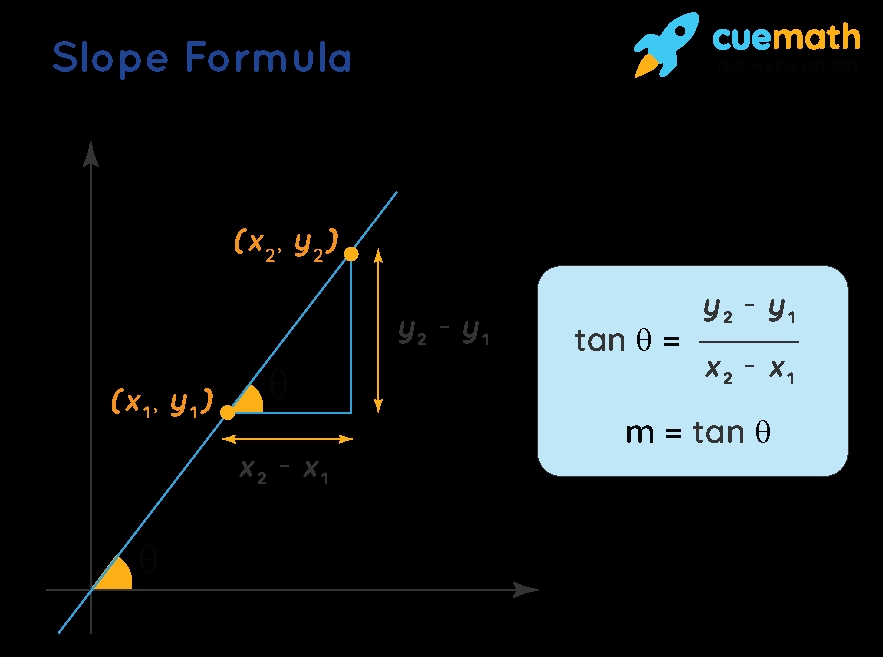
Method 1: Using the Slope Formula
The slope formula is one of the most common methods to find the slope from a graph. The formula is:
m = (y2 - y1) / (x2 - x1)
where (x1, y1) and (x2, y2) are two points on the line.
📝 Note: Make sure to choose two points that are clearly visible on the graph, and use the coordinates of those points to calculate the slope.
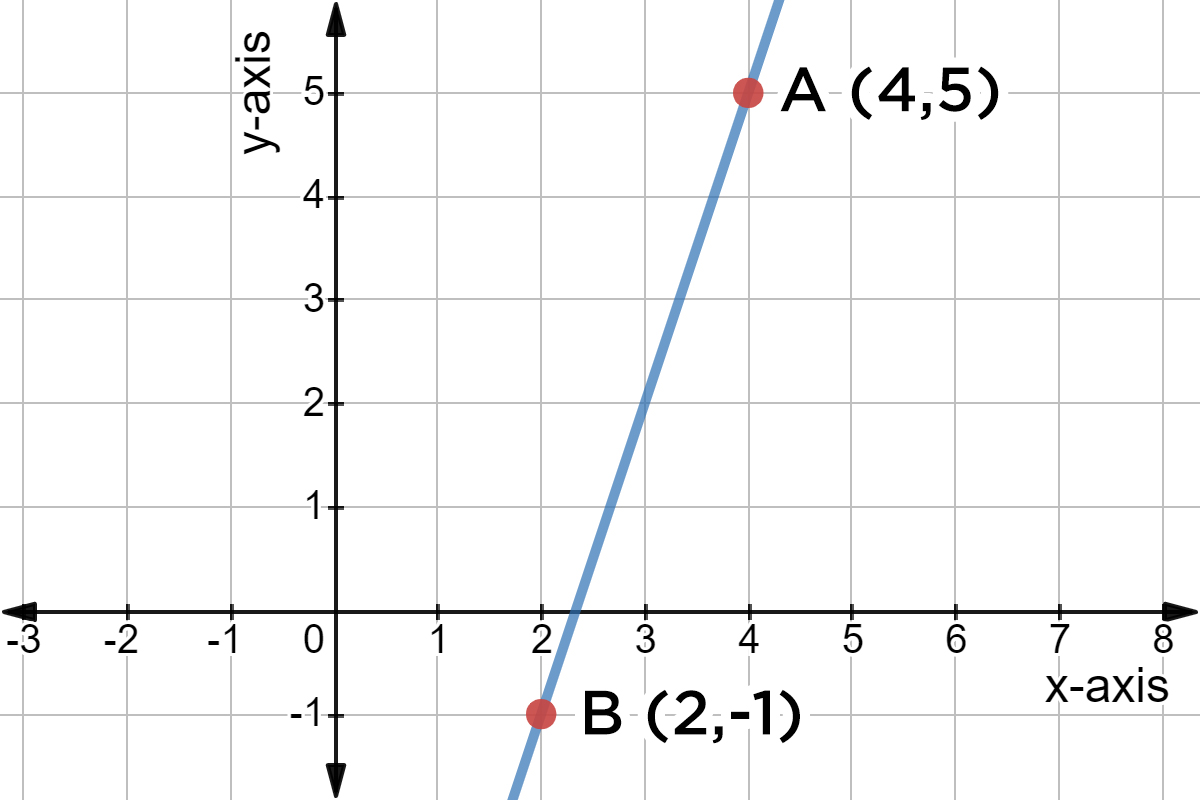
For example, let’s say we have a graph with two points (2, 3) and (4, 5). Using the slope formula, we can calculate the slope as follows:
m = (5 - 3) / (4 - 2) m = 2 / 2 m = 1
Method 2: Counting the Rise and Run
Another way to find the slope from a graph is by counting the rise and run. The rise is the vertical distance between two points, and the run is the horizontal distance. To find the slope, simply divide the rise by the run.
For example, let’s say we have a graph with a line that rises 3 units and runs 4 units. The slope would be:
m = rise / run m = 3 / 4 m = 0.75
📝 Note: Make sure to count the rise and run accurately, and use the same units for both measurements.
Method 3: Using the Graph's Grid
If the graph has a grid, you can use the grid lines to estimate the slope. Simply count the number of grid lines the line crosses vertically (rise) and horizontally (run), and divide the rise by the run.
For example, let’s say we have a graph with a line that crosses 2 vertical grid lines and 3 horizontal grid lines. The slope would be:
m = rise / run m = 2 / 3 m = 0.67
Method 4: Identifying the Slope from a Table
Sometimes, you may have a table of values instead of a graph. You can still find the slope by identifying two points and using the slope formula.
For example, let’s say we have a table with the following values:
| x | y |
|---|---|
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
Using the slope formula, we can calculate the slope as follows:
m = (y2 - y1) / (x2 - x1) m = (3 - 2) / (2 - 1) m = 1 / 1 m = 1
Method 5: Using a Slope Triangle
A slope triangle is a visual representation of the slope, where the horizontal leg represents the run and the vertical leg represents the rise. By creating a slope triangle, you can easily find the slope.
For example, let’s say we have a graph with a line that forms a slope triangle with a run of 3 units and a rise of 2 units. The slope would be:
m = rise / run m = 2 / 3 m = 0.67
| Method | Formula/Description | Example |
|---|---|---|
| 1. Slope Formula | m = (y2 - y1) / (x2 - x1) | m = (5 - 3) / (4 - 2) = 1 |
| 2. Counting Rise and Run | m = rise / run | m = 3 / 4 = 0.75 |
| 3. Using Graph's Grid | m = rise / run | m = 2 / 3 = 0.67 |
| 4. Identifying Slope from Table | m = (y2 - y1) / (x2 - x1) | m = (3 - 2) / (2 - 1) = 1 |
| 5. Using Slope Triangle | m = rise / run | m = 2 / 3 = 0.67 |
In conclusion, finding the slope from a graph is a crucial skill in mathematics, and there are several methods to do so. By using the slope formula, counting the rise and run, using the graph’s grid, identifying the slope from a table, or using a slope triangle, you can easily find the slope of a line. Remember to choose the method that best suits your needs and to always check your work for accuracy.
What is the slope of a horizontal line?
+The slope of a horizontal line is always 0, since the line does not rise or fall vertically.
What is the slope of a vertical line?
+The slope of a vertical line is undefined, since the line rises or falls infinitely vertically.
Can I use a calculator to find the slope?
+Yes, you can use a calculator to find the slope, but make sure to enter the coordinates accurately and use the correct formula.



