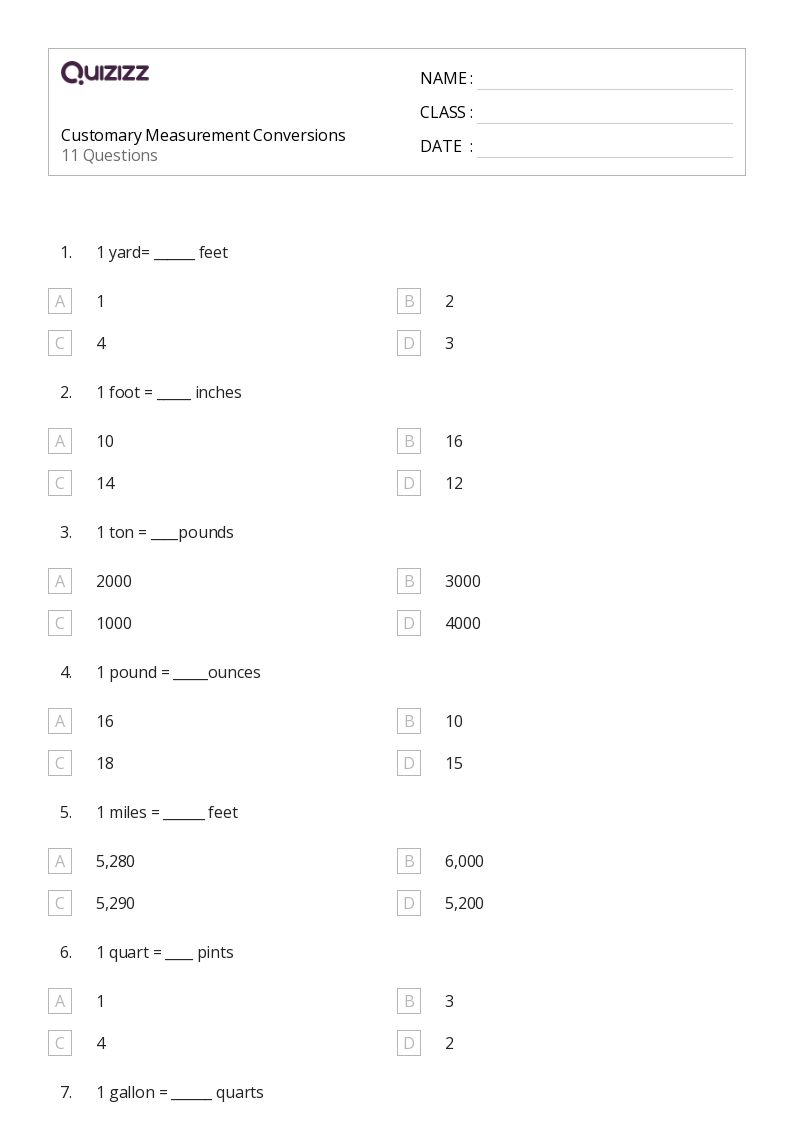
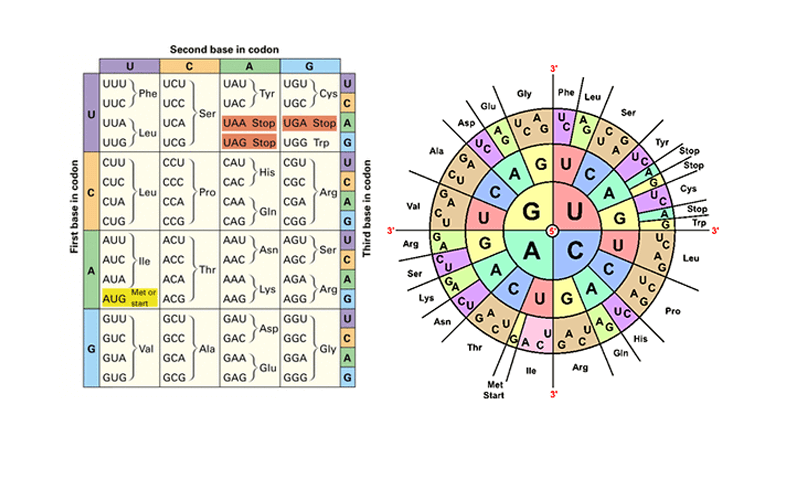
6 Ways to Master Sine and Cosine Laws

Unlocking the Secrets of Sine and Cosine Laws
The sine and cosine laws are fundamental concepts in trigonometry, enabling us to solve complex problems involving triangles. While these laws may seem daunting at first, mastering them can be achieved with practice, patience, and the right approach. In this article, we’ll explore six ways to master sine and cosine laws, helping you to become proficient in no time.
1. Understanding the Basics
Before diving into the laws themselves, it’s essential to understand the basic concepts of trigonometry. Familiarize yourself with the following:
- Angles: Acute, obtuse, right, and straight angles
- Triangles: Types of triangles (acute, right, obtuse), triangle properties (isosceles, equilateral), and triangle relationships (congruent, similar)
- Trigonometric Ratios: Sine, cosine, and tangent (SOH-CAH-TOA)
Key Concepts to Remember:
- Sine (sin) = opposite side / hypotenuse
- Cosine (cos) = adjacent side / hypotenuse
- Tangent (tan) = opposite side / adjacent side
2. Sine Law: A Law of Proportions
The sine law states that the ratio of the length of a side to the sine of its opposite angle is constant for all three sides and angles in a given triangle.
Mathematical Representation:
a / sin(A) = b / sin(B) = c / sin©
where a, b, and c are the sides of the triangle, and A, B, and C are the corresponding angles.
Example Problem:
In a triangle, the length of side a is 5 cm, and the measure of angle A is 30°. If the length of side b is 7 cm, find the measure of angle B.
Solution:
Using the sine law, we can set up the proportion:
5 / sin(30) = 7 / sin(B)
Solving for sin(B), we get:
sin(B) = 7 × sin(30) / 5
B = arcsin(7 × sin(30) / 5)
B ≈ 45.58°
3. Cosine Law: A Law of Vector Addition
The cosine law states that the square of the length of a side is equal to the sum of the squares of the lengths of the other two sides, minus twice the product of those two sides and the cosine of the angle between them.
Mathematical Representation:
c² = a² + b² - 2ab × cos©
where c is the length of the side opposite angle C, and a and b are the lengths of the other two sides.
Example Problem:
In a triangle, the lengths of sides a and b are 6 cm and 8 cm, respectively. If the measure of angle C is 60°, find the length of side c.
Solution:
Using the cosine law, we can plug in the values:
c² = 6² + 8² - 2(6)(8) × cos(60)
c² = 36 + 64 - 96 × 0.5
c² = 100 - 48
c² = 52
c ≈ √52
c ≈ 7.21 cm
4. Practice Problems and Exercises
Practice is key to mastering sine and cosine laws. Try solving various problems, including:
- Find the missing side or angle: Use the sine or cosine law to find the unknown side or angle.
- Check the validity of a triangle: Use the sine or cosine law to verify whether a given triangle is valid.
- Apply to real-world scenarios: Use the sine or cosine law to solve problems involving right triangles, such as finding the height of a building or the distance between two points.
Tips for Practicing:
- Start with simple problems and gradually move to more complex ones.
- Use online resources or worksheets to practice problems.
- Create your own problems or use real-world scenarios to apply the laws.
5. Visualizing the Laws
Visualizing the sine and cosine laws can help you understand and remember them better. Try creating diagrams or graphs to illustrate the laws.
Example Diagram:
Create a diagram showing a triangle with sides a, b, and c, and angles A, B, and C. Draw a line segment representing the side opposite angle C, and label it as c. Draw another line segment representing the side adjacent to angle C, and label it as b. Draw a third line segment representing the hypotenuse, and label it as a.
Visualizing the Sine Law:
Draw a diagram showing the sine law in action. Label the sides and angles of the triangle, and draw a line segment representing the side opposite angle A. Draw another line segment representing the side opposite angle B, and label it as b. Use arrows to show the proportions between the sides and angles.
6. Using Technology to Enhance Learning
Technology can be a great tool to enhance your learning of sine and cosine laws. Utilize online resources, such as:
- Graphing calculators: Use graphing calculators to visualize the sine and cosine laws in action.
- Interactive simulations: Use online simulations to explore the laws and experiment with different values.
- Mathematical software: Use software like GeoGebra or Desmos to create interactive diagrams and explore the laws.
🤔 Note: Remember to always check the validity of your solutions using the laws and theorems you've learned.
In conclusion, mastering sine and cosine laws requires practice, patience, and persistence. By following these six steps, you’ll be well on your way to becoming proficient in these fundamental concepts of trigonometry.
What is the main difference between the sine and cosine laws?
+The main difference between the sine and cosine laws is that the sine law deals with the ratio of the length of a side to the sine of its opposite angle, while the cosine law deals with the square of the length of a side and the cosine of the angle between the other two sides.
How do I know which law to use in a given problem?
+You can use the sine law when you know the length of two sides and the measure of one angle, or when you know the length of one side and the measures of two angles. You can use the cosine law when you know the lengths of two sides and the measure of the angle between them.
Can I use the sine and cosine laws to solve problems involving right triangles?
+Yes, you can use the sine and cosine laws to solve problems involving right triangles. However, in right triangles, the sine and cosine laws simplify to the Pythagorean theorem and the basic trigonometric ratios (SOH-CAH-TOA).
Related Terms:
- Law of Cosines worksheet
- Kuta cosine Law
- Law of Sines Worksheet pdf