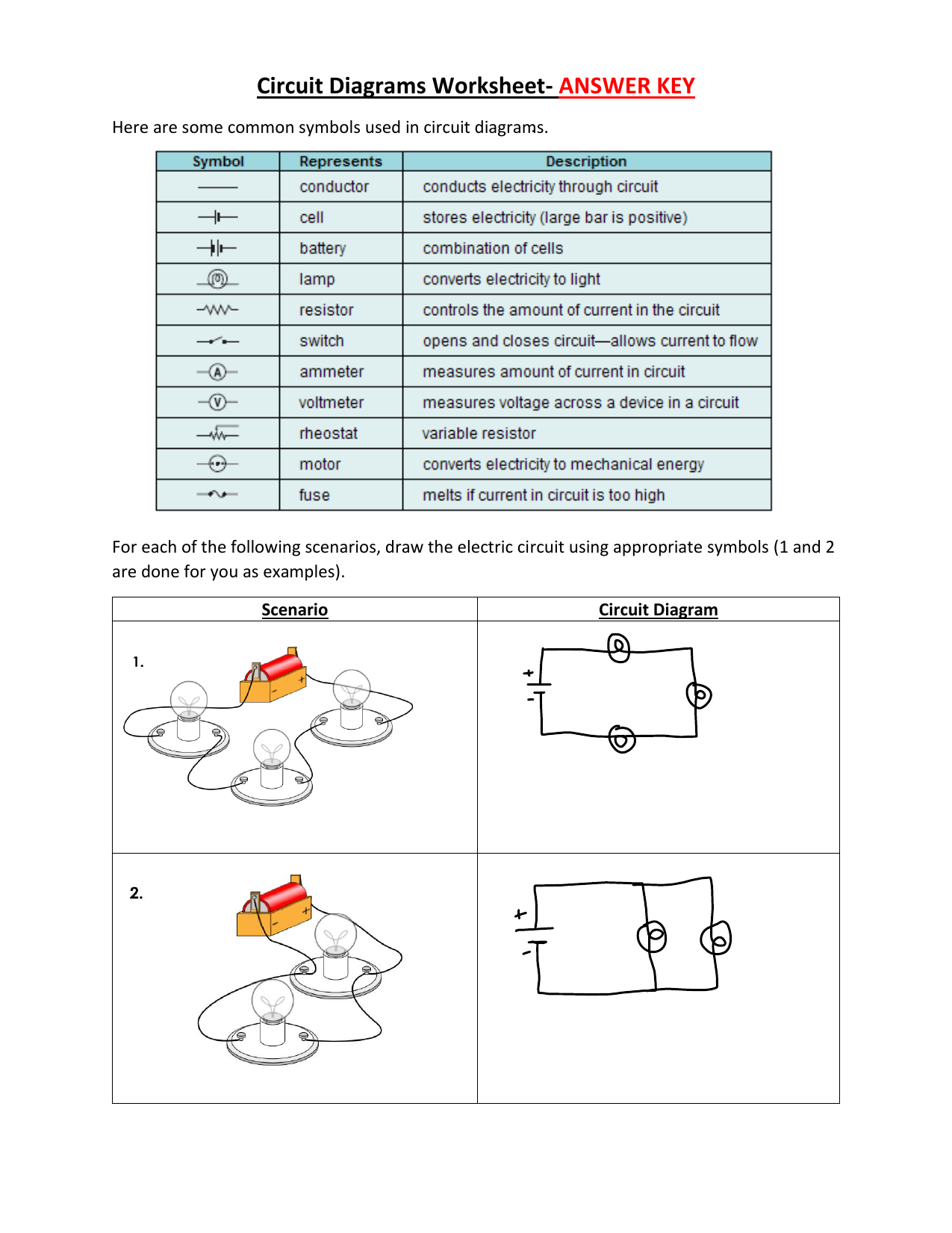
5 Ways to Simplify Radicals Quickly

Simplifying Radicals Made Easy
Simplifying radicals is an essential skill in mathematics, particularly in algebra and geometry. It involves expressing a radical expression in its simplest form, which can be useful for solving equations, graphing functions, and understanding mathematical concepts. In this blog post, we will explore five ways to simplify radicals quickly and efficiently.
Understanding Radicals
Before we dive into the methods of simplifying radicals, let’s first understand what radicals are. A radical is a symbol used to represent the nth root of a number. It consists of a radical sign (√) and an index (n). The index indicates the power to which the number should be raised to obtain the original value. For example, √16 = 4, because 4^2 = 16.
Method 1: Simplifying Radicals Using Perfect Squares
One of the simplest ways to simplify radicals is to look for perfect squares. A perfect square is a number that can be expressed as the square of an integer. For example, 16 is a perfect square because it can be expressed as 4^2. To simplify a radical using perfect squares, follow these steps:
- Identify the perfect square within the radical expression.
- Take the square root of the perfect square.
- Simplify the expression.
For example:
√16 = √(4^2) = 4
🤔 Note: This method only works for square roots (index 2). For other indices, you will need to use different methods.
Method 2: Simplifying Radicals Using Prime Factorization
Another way to simplify radicals is to use prime factorization. Prime factorization involves breaking down a number into its prime factors. To simplify a radical using prime factorization, follow these steps:
- Factor the number within the radical expression into its prime factors.
- Look for pairs of identical prime factors.
- Take the square root of each pair of identical prime factors.
- Simplify the expression.
For example:
√48 = √(2^4 × 3) = √(2^2 × 2^2 × 3) = 2√(2 × 3) = 2√6
Method 3: Simplifying Radicals Using the Conjugate Pair
The conjugate pair method is useful for simplifying radicals that involve addition or subtraction within the radical expression. To simplify a radical using the conjugate pair method, follow these steps:
- Identify the conjugate pair within the radical expression.
- Multiply the radical expression by the conjugate pair.
- Simplify the expression.
For example:
√(2 + √3) = √(2 + √3) × √(2 - √3) / √(2 - √3) = √(4 - 3) / √(2 - √3) = √1 / √(2 - √3) = 1 / √(2 - √3)
Method 4: Simplifying Radicals Using the Rationalizing Method
The rationalizing method involves multiplying the radical expression by a clever form of 1 to eliminate the radical. To simplify a radical using the rationalizing method, follow these steps:
- Identify the radical expression that needs to be rationalized.
- Multiply the radical expression by a clever form of 1.
- Simplify the expression.
For example:
√(2⁄3) = √(2⁄3) × √(3⁄3) = √(2 × 3⁄3 × 3) = √6/3
Method 5: Simplifying Radicals Using Online Tools
Finally, there are online tools available that can simplify radicals quickly and efficiently. These tools can be useful for checking your work or for simplifying complex radicals. Some popular online tools include Wolfram Alpha, Mathway, and Symbolab.
As we can see, simplifying radicals can be done in various ways. By mastering these five methods, you can quickly and efficiently simplify radicals and improve your math skills.
The key to simplifying radicals quickly is to be able to recognize the different types of radicals and apply the appropriate method. With practice and patience, you can become proficient in simplifying radicals and tackle more complex math problems.
What is the difference between a radical and a square root?
+A radical is a symbol used to represent the nth root of a number, while a square root is a specific type of radical with an index of 2.
How do I simplify a radical expression with multiple indices?
+To simplify a radical expression with multiple indices, you can use the prime factorization method or the rationalizing method.
Can I simplify radicals using online tools?
+Yes, there are online tools available that can simplify radicals quickly and efficiently, such as Wolfram Alpha, Mathway, and Symbolab.
Related Terms:
- Simplifying Radicals Worksheet pdf
- Simplifying Radicals Worksheet Kuta Software