Simplifying Fractions: Simplest Form Worksheet for Easy Practice

Simplifying Fractions: A Comprehensive Guide
Simplifying fractions is an essential math concept that involves reducing a fraction to its simplest form. In this article, we will delve into the world of fractions, understand what simplifying fractions means, and learn how to simplify them with ease.
What are Fractions?
Fractions are a way to represent part of a whole. They consist of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator tells us how many equal parts we have, while the denominator tells us how many parts the whole is divided into.
What is Simplifying Fractions?
Simplifying fractions means reducing a fraction to its simplest form, where the numerator and denominator have no common factors other than 1. In other words, simplifying fractions involves finding the smallest possible numerator and denominator that still represent the same proportion.
Why Simplify Fractions?
Simplifying fractions is important for several reasons:
- Easier calculations: Simplified fractions make calculations easier and faster.
- Improved understanding: Simplified fractions help us understand the proportion better.
- Accurate comparisons: Simplified fractions enable us to compare fractions accurately.
How to Simplify Fractions
Simplifying fractions involves dividing both the numerator and denominator by their greatest common divisor (GCD). Here’s a step-by-step guide:
- Find the GCD: Find the greatest common divisor of the numerator and denominator.
- Divide both numbers: Divide both the numerator and denominator by the GCD.
- Write the simplified fraction: Write the simplified fraction with the new numerator and denominator.
📝 Note: Make sure to check if the fraction is already in its simplest form before attempting to simplify it.
Examples of Simplifying Fractions
Let’s practice simplifying fractions with some examples:
- Example 1: Simplify the fraction 6⁄8.
- Find the GCD: 2
- Divide both numbers: 6 ÷ 2 = 3, 8 ÷ 2 = 4
- Write the simplified fraction: 3⁄4
- Example 2: Simplify the fraction 12⁄16.
- Find the GCD: 4
- Divide both numbers: 12 ÷ 4 = 3, 16 ÷ 4 = 4
- Write the simplified fraction: 3⁄4
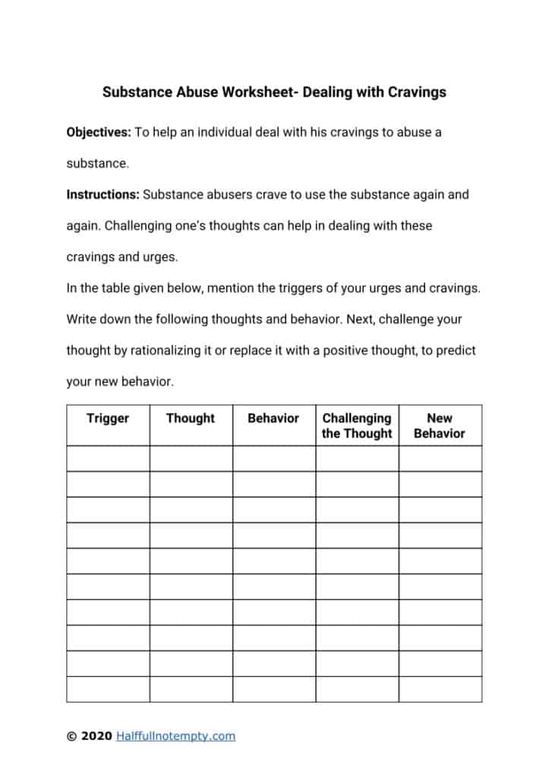
Simplest Form Worksheet
Practice simplifying fractions with our simplest form worksheet:
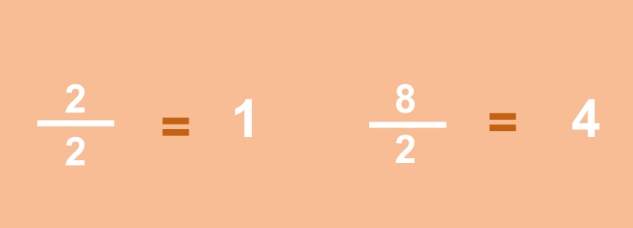
| Fraction | Simplified Fraction |
|---|---|
| 4⁄6 | |
| 8⁄12 | |
| 3⁄9 | |
| 6⁄10 | |
| 9⁄12 |
📝 Note: Try to simplify the fractions on your own before checking the answers.
Answers
| Fraction | Simplified Fraction |
|---|---|
| 4⁄6 | 2⁄3 |
| 8⁄12 | 2⁄3 |
| 3⁄9 | 1⁄3 |
| 6⁄10 | 3⁄5 |
| 9⁄12 | 3⁄4 |
Conclusion
Simplifying fractions is an essential math concept that helps us reduce fractions to their simplest form. By following the steps outlined in this article, you can simplify fractions with ease and improve your math skills. Remember to practice regularly and use our simplest form worksheet to reinforce your understanding.
What is the greatest common divisor (GCD)?
+The greatest common divisor (GCD) is the largest number that divides both the numerator and denominator without leaving a remainder.
How do I know if a fraction is already in its simplest form?
+If the numerator and denominator have no common factors other than 1, the fraction is already in its simplest form.
Can I simplify a fraction by dividing both numbers by any number?
+No, you can only simplify a fraction by dividing both numbers by their greatest common divisor (GCD).
Related Terms:
- Multiplying Fractions worksheet pdf
- Fraction Worksheet Grade 5
- Subtracting fractions Worksheet
- Fraction addition and subtraction worksheet
- Addition fraction Worksheet