5 Ways to Master Similar Triangles

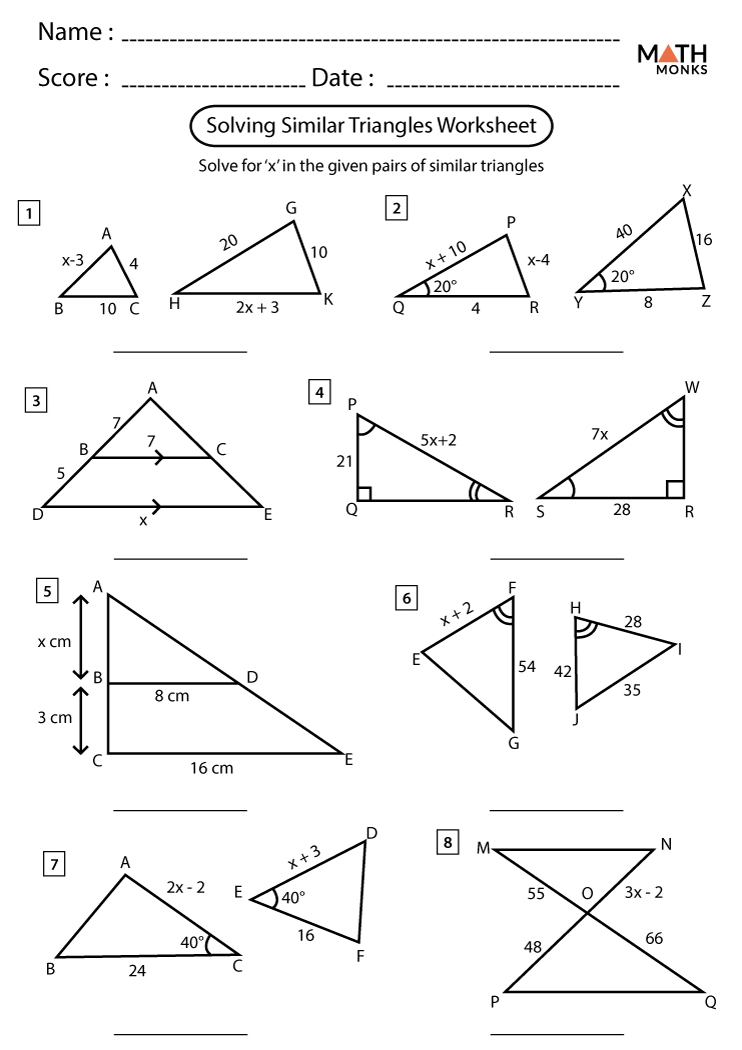
Mastering similar triangles is an essential skill for any math student or enthusiast. Similar triangles are triangles that have the same shape, but not necessarily the same size. They can be used to solve a wide range of problems, from simple geometry to complex trigonometry. In this article, we will explore five ways to master similar triangles.

Understanding Similar Triangles

Before we dive into the five ways to master similar triangles, it’s essential to understand what similar triangles are and how they work. Similar triangles are triangles that have the same shape, but not necessarily the same size. This means that the corresponding angles are equal, and the corresponding sides are in proportion.

For example, consider two triangles, ΔABC and ΔDEF, with the following properties:

• ∠A = ∠D
• ∠B = ∠E
• ∠C = ∠F
• AB/DE = BC/EF = AC/DF

In this case, ΔABC and ΔDEF are similar triangles. The corresponding angles are equal, and the corresponding sides are in proportion.

Method 1: Using Proportional Sides

One of the most common ways to work with similar triangles is to use proportional sides. If two triangles are similar, the corresponding sides are in proportion. This means that if you know the length of one side of one triangle, you can use the proportion to find the length of the corresponding side of the other triangle.

For example, consider the following problem:

ΔABC and ΔDEF are similar triangles. If AB = 6 cm, BC = 8 cm, and DE = 9 cm, find the length of EF.

Using proportional sides, we can set up the following proportion:

AB/DE = BC/EF

Substituting the given values, we get:

⁶⁄₉ = 8/EF

Cross-multiplying and solving for EF, we get:

EF = 12 cm

📝 Note: When working with proportional sides, make sure to label the corresponding sides correctly. This will help you set up the proportion correctly and avoid mistakes.

Method 2: Using Angle-Angle (AA) Similarity

Another way to work with similar triangles is to use angle-angle (AA) similarity. If two triangles have two pairs of congruent angles, the triangles are similar.

For example, consider the following problem:

ΔABC and ΔDEF are two triangles with the following properties:

• ∠A = ∠D
• ∠B = ∠E

If AB = 5 cm and DE = 7 cm, find the length of BC.

Using AA similarity, we can conclude that ΔABC and ΔDEF are similar triangles. Since the corresponding sides are in proportion, we can set up the following proportion:

AB/DE = BC/EF

Substituting the given values, we get:

⁵⁄₇ = BC/EF

Cross-multiplying and solving for BC, we get:

BC = 7.5 cm

Method 3: Using Side-Angle-Side (SAS) Similarity

Side-angle-side (SAS) similarity is another way to work with similar triangles. If two triangles have two pairs of congruent sides and the included angle is congruent, the triangles are similar.

For example, consider the following problem:

ΔABC and ΔDEF are two triangles with the following properties:

• AB = DE
• BC = EF
• ∠B = ∠E

If AB = 4 cm and BC = 6 cm, find the length of AC.

Using SAS similarity, we can conclude that ΔABC and ΔDEF are similar triangles. Since the corresponding sides are in proportion, we can set up the following proportion:

AB/DE = AC/DF

Substituting the given values, we get:

⁴⁄₄ = AC/6

Cross-multiplying and solving for AC, we get:

AC = 6 cm

Method 4: Using Right Triangle Trigonometry

Right triangle trigonometry is another way to work with similar triangles. If two triangles are right triangles and the hypotenuse is congruent, the triangles are similar.

For example, consider the following problem:

ΔABC and ΔDEF are two right triangles with the following properties:

• ∠A = ∠D = 90°
• AB = DE = 3 cm

If AC = 4 cm, find the length of DF.

Using right triangle trigonometry, we can conclude that ΔABC and ΔDEF are similar triangles. Since the corresponding sides are in proportion, we can set up the following proportion:

AB/DE = AC/DF

Substituting the given values, we get:

³⁄₃ = 4/DF

Cross-multiplying and solving for DF, we get:

DF = 4 cm

Method 5: Using Triangle Similarity Theorems

Finally, there are several triangle similarity theorems that can be used to work with similar triangles. These theorems include:

• AA similarity theorem: If two triangles have two pairs of congruent angles, the triangles are similar.
• SAS similarity theorem: If two triangles have two pairs of congruent sides and the included angle is congruent, the triangles are similar.
• SSS similarity theorem: If two triangles have three pairs of congruent sides, the triangles are similar.

For example, consider the following problem:

ΔABC and ΔDEF are two triangles with the following properties:

• AB = DE
• BC = EF
• AC = DF

Using the SSS similarity theorem, we can conclude that ΔABC and ΔDEF are similar triangles.

📝 Note: Triangle similarity theorems can be used to prove that two triangles are similar, but they cannot be used to find the length of a side or the measure of an angle.

To summarize, mastering similar triangles requires a combination of skills, including understanding proportional sides, angle-angle similarity, side-angle-side similarity, right triangle trigonometry, and triangle similarity theorems. By practicing these skills and using them in a variety of problems, you can become proficient in working with similar triangles.

Related Terms:

• Similar triangles angles Worksheet
• Triangle similarity Worksheet PDF
• Parts of similar triangles Worksheet
• Triangle proportionality theorem worksheet