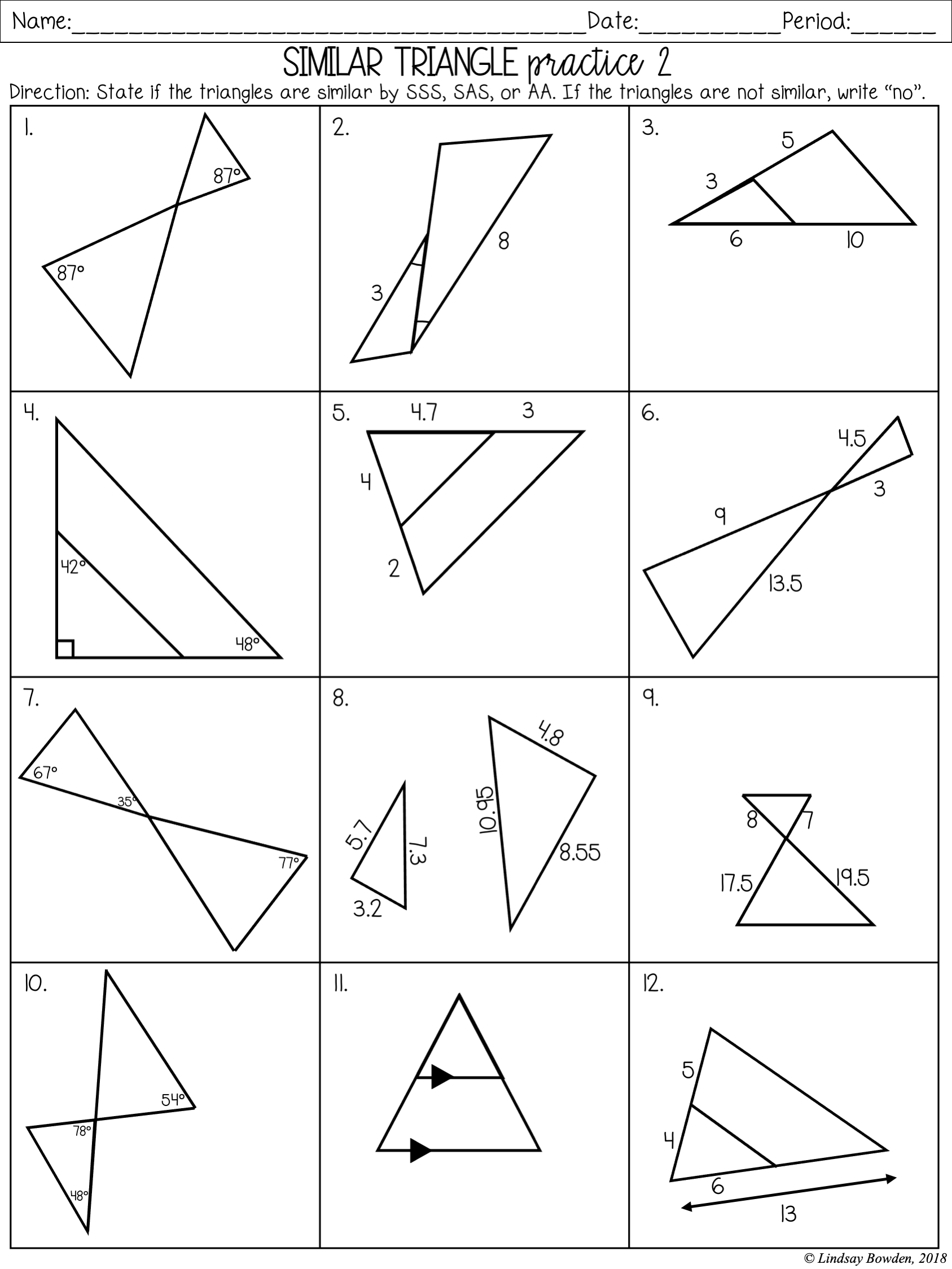
Similar Triangles Worksheets

Understanding similar triangles is a crucial concept in geometry, and working through worksheets can help reinforce this understanding. In this blog post, we’ll delve into the concept of similar triangles, explore their properties, and provide examples of worksheets to practice.
What are Similar Triangles?
Similar triangles are triangles that have the same shape, but not necessarily the same size. This means that corresponding angles are equal and the corresponding sides are in proportion. Similar triangles are denoted by the symbol ~.
Properties of Similar Triangles
Similar triangles have several key properties:
- Angle-Angle (AA) Similarity: If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.
- Side-Angle-Side (SAS) Similarity: If two sides of one triangle are proportional to two sides of another triangle, and the included angles are congruent, then the triangles are similar.
- Side-Side-Side (SSS) Similarity: If three sides of one triangle are proportional to three sides of another triangle, then the triangles are similar.
Similar Triangles Theorems
There are several theorems that relate to similar triangles:
- Similar Triangles Theorem: If two triangles are similar, then their corresponding sides are proportional and their corresponding angles are congruent.
- Proportionality Theorem: If two triangles are similar, then the ratio of the lengths of their corresponding sides is equal to the ratio of their corresponding altitudes.
Worksheets for Practicing Similar Triangles
Here are some examples of worksheets to practice similar triangles:
Worksheet 1: Identifying Similar Triangles
Identify whether the following triangles are similar:
| Triangle 1 | Triangle 2 |
|---|---|
| ∆ABC | ∆DEF |
| ∆GHI | ∆JKL |
| ∆MNO | ∆PQR |
Answer Key
- ∆ABC ~ ∆DEF (AA similarity)
- ∆GHI ~ ∆JKL (SAS similarity)
- ∆MNO ~ ∆PQR (SSS similarity)
Worksheet 2: Finding Proportional Sides
Find the proportional sides of the following similar triangles:
| Triangle 1 | Triangle 2 | Proportional Sides |
|---|---|---|
| ∆ABC | ∆DEF | AB/DE = BC/EF = AC/DF |
| ∆GHI | ∆JKL | GH/JK = HI/KL = GI/JL |
| ∆MNO | ∆PQR | MN/PQ = NO/QR = MO/PR |
Answer Key
- AB/DE = BC/EF = AC/DF = 2⁄3
- GH/JK = HI/KL = GI/JL = 3⁄4
- MN/PQ = NO/QR = MO/PR = 1⁄2
Worksheet 3: Solving Similar Triangles
Solve for x in the following similar triangles:
| Triangle 1 | Triangle 2 | Equation |
|---|---|---|
| ∆ABC | ∆DEF | AB/DE = BC/EF = AC/DF = x/4 |
| ∆GHI | ∆JKL | GH/JK = HI/KL = GI/JL = 2x/5 |
| ∆MNO | ∆PQR | MN/PQ = NO/QR = MO/PR = x/3 |
Answer Key
- x = 6
- x = 10⁄3
- x = 9⁄2
Tips and Variations
- Use real-world examples, such as architecture or engineering, to illustrate the concept of similar triangles.
- Include more complex problems, such as finding the area or perimeter of similar triangles.
- Use graphing software or online tools to explore similar triangles and their properties.
Important Notes
💡 Note: When working with similar triangles, it's essential to identify the corresponding sides and angles to determine the proportionality.
📝 Note: Use the theorems and properties of similar triangles to solve problems, rather than just relying on memorization.
By working through these worksheets and practicing similar triangles, you’ll become more confident in your ability to identify and solve problems involving these fundamental geometric shapes.
In conclusion, similar triangles are an essential concept in geometry, and mastering their properties and theorems can help you tackle a wide range of problems. By incorporating worksheets and real-world examples into your learning, you’ll be well on your way to becoming proficient in similar triangles.
What is the definition of similar triangles?
+
Similar triangles are triangles that have the same shape, but not necessarily the same size. This means that corresponding angles are equal and the corresponding sides are in proportion.
What are the properties of similar triangles?
+
The properties of similar triangles include angle-angle (AA) similarity, side-angle-side (SAS) similarity, and side-side-side (SSS) similarity.
How can I practice similar triangles?
+
You can practice similar triangles by working through worksheets, such as the ones provided in this blog post, and by using real-world examples to illustrate the concept.



