5 Ways to Master Coordinate Plane Reflections
Understanding Coordinate Plane Reflections
Reflections in the coordinate plane are a fundamental concept in geometry, and mastering them is essential for problem-solving and critical thinking. In this article, we will explore five ways to master coordinate plane reflections, making it easier for you to understand and apply this concept in various mathematical contexts.
1. Visualizing Reflections
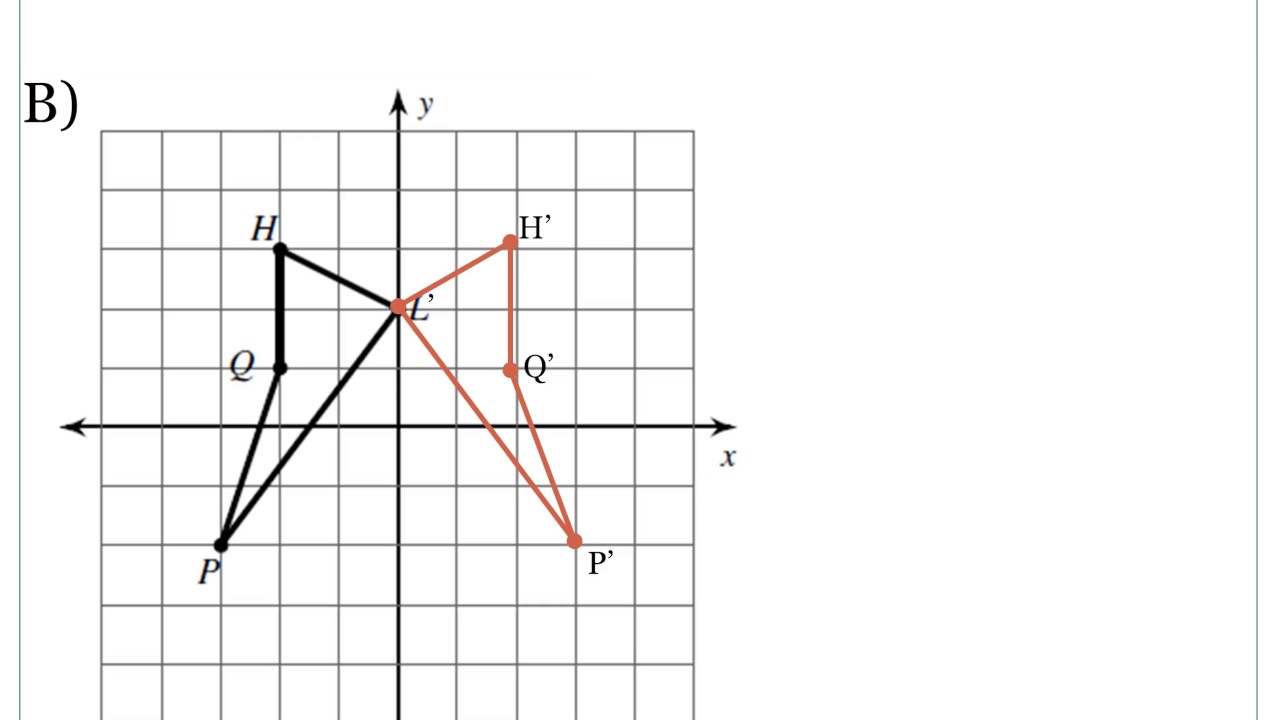
Visualizing reflections is the first step to mastering them. Imagine a mirror placed on the coordinate plane, and an object (point, line, or shape) reflected across it. The mirror can be any line, including the x-axis, y-axis, or a diagonal line. When an object is reflected, its image appears on the other side of the mirror, creating a symmetrical effect.
To visualize reflections effectively, try the following:
- Use graph paper to draw a coordinate plane and a mirror line.
- Plot a point or shape on one side of the mirror.
- Reflect the point or shape across the mirror, creating a symmetrical image.
- Label the original point or shape as “pre-image” and the reflected point or shape as “image.”
📝 Note: The mirror line can be any line, but it's essential to identify the type of reflection (e.g., reflection across the x-axis, y-axis, or a diagonal line) to determine the correct image.
2. Identifying Reflection Types
There are several types of reflections in the coordinate plane, including:
- Reflection across the x-axis
- Reflection across the y-axis
- Reflection across a diagonal line (e.g., y = x or y = -x)
- Reflection across a horizontal or vertical line (e.g., x = 2 or y = 3)
To identify the type of reflection, analyze the mirror line and the pre-image. Ask yourself:
- Is the mirror line horizontal (x-axis) or vertical (y-axis)?
- Is the mirror line a diagonal line (e.g., y = x or y = -x)?
- Is the mirror line a horizontal or vertical line (e.g., x = 2 or y = 3)?
By identifying the type of reflection, you can determine the correct image and apply the necessary transformation.
3. Applying Reflection Rules
To reflect a point or shape across a mirror line, apply the following rules:
- Reflection across the x-axis: (x, y) → (x, -y)
- Reflection across the y-axis: (x, y) → (-x, y)
- Reflection across a diagonal line (y = x): (x, y) → (y, x)
- Reflection across a diagonal line (y = -x): (x, y) → (-y, -x)
- Reflection across a horizontal line (x = a): (x, y) → (2a - x, y)
- Reflection across a vertical line (y = b): (x, y) → (x, 2b - y)
Apply these rules to reflect points, lines, or shapes across various mirror lines.
📝 Note: When reflecting across a diagonal line, the x and y coordinates swap places, but the signs may change depending on the type of diagonal line.
4. Using Coordinates to Reflect Shapes
To reflect a shape across a mirror line, you can use coordinates to determine the image. Here’s a step-by-step approach:
- Identify the type of reflection and the mirror line.
- Label the vertices of the shape with coordinates.
- Apply the reflection rules to each vertex, using the correct transformation.
- Plot the reflected vertices on the coordinate plane.
- Draw the reflected shape by connecting the vertices.

| Original Shape | Reflected Shape |
|---|---|
| (2, 3) | (2, -3) |
| (4, 5) | (4, -5) |
| (6, 7) | (6, -7) |
📝 Note: When reflecting a shape, make sure to apply the same transformation to all vertices.
5. Solving Reflection Problems
To become proficient in coordinate plane reflections, practice solving various problems, such as:
- Reflecting points, lines, or shapes across different mirror lines.
- Identifying the type of reflection and applying the correct transformation.
- Using coordinates to reflect shapes and determine the image.
Here’s an example problem:
Reflect the point (3, 4) across the line y = x.
Solution: Since the mirror line is a diagonal line (y = x), we swap the x and y coordinates: (3, 4) → (4, 3).
By mastering these five ways to master coordinate plane reflections, you’ll become proficient in visualizing, identifying, and applying reflections in various mathematical contexts.
In the world of geometry, coordinate plane reflections are a fundamental concept that can help you solve complex problems and think critically. By understanding how to reflect points, lines, and shapes across different mirror lines, you’ll develop a deeper appreciation for the beauty and symmetry of geometry.
What is the main concept of coordinate plane reflections?
+Coordinate plane reflections involve reflecting points, lines, or shapes across a mirror line on the coordinate plane, creating a symmetrical effect.
What are the different types of reflections in the coordinate plane?
+There are several types of reflections, including reflections across the x-axis, y-axis, diagonal lines, and horizontal or vertical lines.
How do you reflect a point or shape across a mirror line?
+To reflect a point or shape, apply the correct transformation rule based on the type of reflection, using coordinates to determine the image.
Related Terms:
- Reflection Worksheet PDF with answers