Reflections Geometry Worksheet Solutions
Reflections in Geometry: A Comprehensive Guide
In geometry, a reflection is a type of rigid motion that flips a shape over a line, called the line of reflection. The line of reflection is the perpendicular bisector of the line segment connecting a point on the shape with its image after the reflection. In this article, we will delve into the world of reflections in geometry, exploring the concept, properties, and applications of reflections.
What is a Reflection in Geometry?
A reflection in geometry is a transformation that maps every point of a shape to a corresponding point on the opposite side of a fixed line, called the line of reflection. The line of reflection is the perpendicular bisector of the line segment connecting a point on the shape with its image after the reflection.
Key Properties of Reflections:
- Line of Reflection: The line of reflection is the perpendicular bisector of the line segment connecting a point on the shape with its image after the reflection.
- Image and Preimage: The image is the result of the reflection, while the preimage is the original shape before the reflection.
- Congruent Shapes: Reflections preserve the size and shape of the original figure, resulting in congruent shapes.
Types of Reflections
There are several types of reflections in geometry, including:
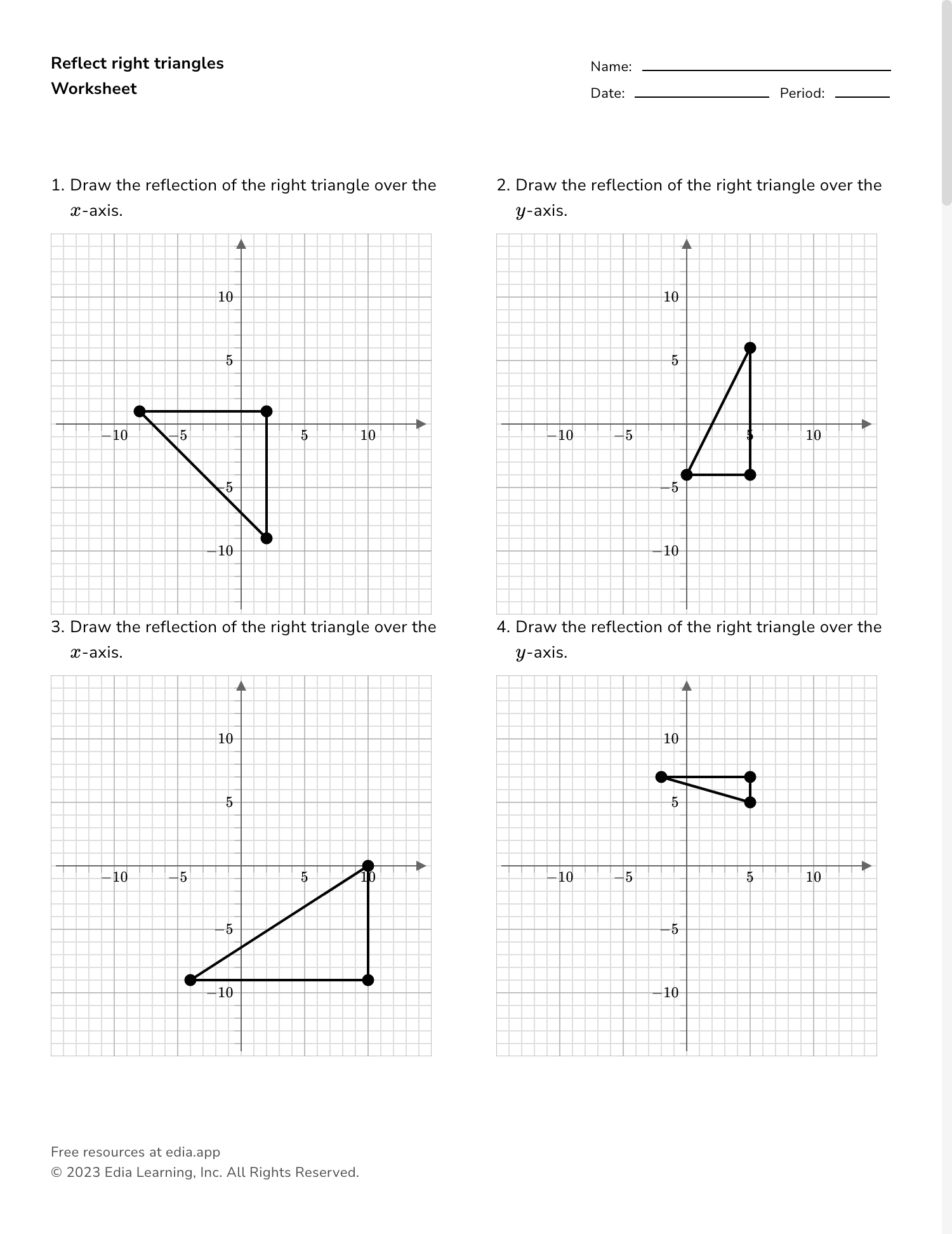
- Reflection across the x-axis: This type of reflection flips a shape over the x-axis.
- Reflection across the y-axis: This type of reflection flips a shape over the y-axis.
- Reflection across a diagonal: This type of reflection flips a shape over a diagonal line.
How to Reflect a Shape
To reflect a shape, follow these steps:
- Identify the line of reflection.
- Draw a line segment connecting a point on the shape with its image after the reflection.
- Find the midpoint of the line segment.
- Draw a perpendicular line through the midpoint.
- The resulting line is the line of reflection.
- Use the line of reflection to flip the shape over, creating the image.
💡 Note: When reflecting a shape, make sure to label the image and preimage correctly to avoid confusion.
Real-World Applications of Reflections
Reflections have numerous real-world applications, including:
- Symmetry: Reflections are used to create symmetrical designs in art, architecture, and engineering.
- Optics: Reflections are used to study the behavior of light and its interactions with matter.
- Computer Graphics: Reflections are used to create realistic graphics and animations in video games and movies.
Reflections in Coordinate Geometry
In coordinate geometry, reflections can be represented using coordinate transformations. For example:
- Reflection across the x-axis: (x, y) → (x, -y)
- Reflection across the y-axis: (x, y) → (-x, y)
- Reflection across a diagonal: (x, y) → (-y, -x)
Common Mistakes to Avoid
When working with reflections, common mistakes to avoid include:
- Incorrect line of reflection: Make sure to identify the correct line of reflection to avoid errors.
- Labeling mistakes: Label the image and preimage correctly to avoid confusion.
📝 Note: Practice makes perfect. Make sure to practice reflecting shapes to become proficient in this concept.
To summarize, reflections in geometry are a fundamental concept that involves flipping a shape over a line of reflection. By understanding the properties, types, and applications of reflections, you can master this concept and apply it to real-world problems.
What is the line of reflection in a reflection?
+
The line of reflection is the perpendicular bisector of the line segment connecting a point on the shape with its image after the reflection.
What is the difference between an image and a preimage?
+
The image is the result of the reflection, while the preimage is the original shape before the reflection.
How do I reflect a shape across the x-axis?
+
To reflect a shape across the x-axis, multiply the y-coordinate of each point by -1.
Related Terms:
- Dilation worksheet with answers pdf
- Worksheet transformations geometry
- Transformation Worksheet pdf
- Scale factor worksheet
- Tangent circle worksheet pdf



