Mastering Quadratic Factorisation with Ease
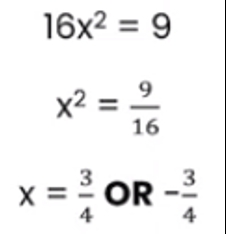
Unlocking the Secrets of Quadratic Factorisation
Quadratic factorisation is a fundamental concept in algebra, and it’s a skill that can be mastered with practice and patience. In this article, we’ll delve into the world of quadratic factorisation, exploring its basics, techniques, and tips to help you become a pro in no time.
What is Quadratic Factorisation?
Quadratic factorisation is the process of expressing a quadratic expression in the form of (ax + b)(cx + d), where a, b, c, and d are constants. It’s a crucial technique in solving quadratic equations, which are equations that have a squared variable, usually x.
Why is Quadratic Factorisation Important?
Quadratic factorisation is essential in various areas of mathematics, science, and engineering. It helps in solving quadratic equations, which are used to model real-world problems, such as projectile motion, electrical circuits, and population growth.
Basic Techniques of Quadratic Factorisation
There are several techniques used in quadratic factorisation, including:
- Factoring by inspection: This involves finding two numbers whose product is the constant term and whose sum is the coefficient of the linear term.
- Factoring by grouping: This involves grouping the terms of the quadratic expression and factoring out common factors.
- Factoring using the quadratic formula: This involves using the quadratic formula to find the roots of the quadratic equation and then factoring the expression.
Factoring by Inspection
Factoring by inspection is a simple technique used to factorise quadratic expressions of the form x^2 + bx + c. It involves finding two numbers whose product is c and whose sum is b.
Example: Factorise x^2 + 5x + 6
- Find two numbers whose product is 6 and whose sum is 5.
- The numbers are 2 and 3.
- Write the factored form: (x + 2)(x + 3)
Factoring by Grouping
Factoring by grouping involves grouping the terms of the quadratic expression and factoring out common factors.
Example: Factorise x^2 + 2x + 3x + 6
- Group the terms: x^2 + 2x + 3x + 6 = (x^2 + 2x) + (3x + 6)
- Factor out common factors: (x^2 + 2x) + (3x + 6) = x(x + 2) + 3(x + 2)
- Factor out the common binomial factor: x(x + 2) + 3(x + 2) = (x + 3)(x + 2)
Factoring using the Quadratic Formula
The quadratic formula is used to find the roots of a quadratic equation. Once the roots are found, the quadratic expression can be factored.
Example: Factorise x^2 + 4x + 4
- Use the quadratic formula to find the roots: x = (-b ± √(b^2 - 4ac)) / 2a
- Simplify the expression: x = (-4 ± √(16 - 16)) / 2
- Simplify further: x = (-4 ± 0) / 2
- Find the roots: x = -2
- Factor the expression: (x + 2)(x + 2)
Tips and Tricks for Mastering Quadratic Factorisation
- Practice, practice, practice: The more you practice, the more comfortable you’ll become with the techniques.
- Start with simple expressions: Begin with simple quadratic expressions and gradually move on to more complex ones.
- Use visual aids: Visual aids, such as graphs and charts, can help you understand the concept better.
- Break down complex expressions: Break down complex quadratic expressions into simpler ones to make factoring easier.
📝 Note: Quadratic factorisation can be challenging, but with persistence and practice, you can master it.
Common Mistakes to Avoid
- Incorrect signs: Make sure to use the correct signs when factoring.
- Incorrect grouping: Be careful when grouping terms, as incorrect grouping can lead to incorrect factoring.
- Forgetting to factor out common factors: Always factor out common factors to simplify the expression.
🚨 Note: Avoid these common mistakes to ensure accurate factoring.
Real-World Applications of Quadratic Factorisation
Quadratic factorisation has numerous real-world applications, including:
- Projectile motion: Quadratic equations are used to model the trajectory of projectiles, such as the path of a thrown ball.
- Electrical circuits: Quadratic equations are used to model the behavior of electrical circuits, such as the resistance and capacitance of a circuit.
- Population growth: Quadratic equations are used to model population growth, such as the growth of a bacterial colony.
In conclusion, mastering quadratic factorisation requires practice, patience, and persistence. With the techniques and tips outlined in this article, you’ll be well on your way to becoming a pro in quadratic factorisation. Remember to practice regularly, use visual aids, and avoid common mistakes to ensure accurate factoring.
What is the difference between factoring by inspection and factoring by grouping?
+Factoring by inspection involves finding two numbers whose product is the constant term and whose sum is the coefficient of the linear term. Factoring by grouping involves grouping the terms of the quadratic expression and factoring out common factors.
When should I use the quadratic formula to factorise a quadratic expression?
+Use the quadratic formula to factorise a quadratic expression when the expression cannot be factored using other methods, such as factoring by inspection or factoring by grouping.
What are some common mistakes to avoid when factoring quadratic expressions?
+Common mistakes to avoid when factoring quadratic expressions include incorrect signs, incorrect grouping, and forgetting to factor out common factors.