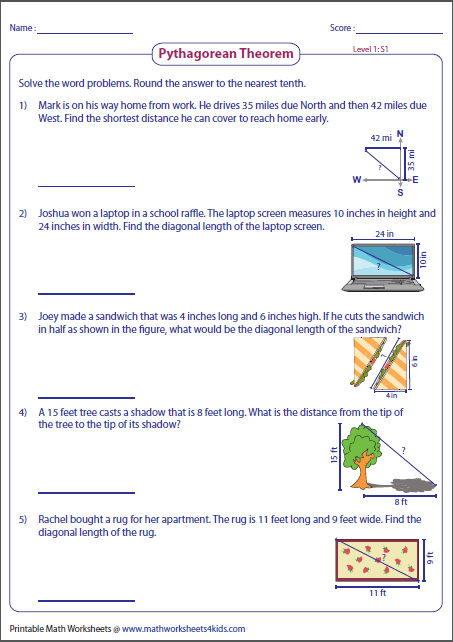
Pythagorean Theorem Word Problems Worksheets With Answers
Unlocking the Secrets of the Pythagorean Theorem through Word Problems
The Pythagorean theorem is a fundamental concept in geometry, and its applications are numerous in various fields, including physics, engineering, and architecture. To help students master this concept, we will explore word problems that require the use of the Pythagorean theorem. In this article, we will delve into the world of word problems, providing you with worksheets and answers to help you better understand this concept.
What is the Pythagorean Theorem?
The Pythagorean theorem is a mathematical concept that describes the relationship between the lengths of the sides of a right-angled triangle. The theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
Mathematically, this can be expressed as:
a² + b² = c²
where:
- a and b are the lengths of the two sides that form the right angle
- c is the length of the hypotenuse (the side opposite the right angle)
Word Problems Involving the Pythagorean Theorem
Word problems are an excellent way to apply the Pythagorean theorem to real-world scenarios. Here are a few examples:
Example 1: The Ladder Problem
Tom is a construction worker who needs to reach the top of a building that is 12 meters high. He has a ladder that is 5 meters long. How far from the base of the building should Tom place the ladder so that it reaches the top of the building?
Example 2: The Bridge Problem
A bridge spans a river, and the length of the bridge is 30 meters. The height of the bridge above the water is 10 meters. How wide is the river?
Example 3: The Building Problem
A building has a rectangular base with a length of 20 meters and a width of 15 meters. A diagonal path connects two opposite corners of the base. What is the length of this diagonal path?
Solutions to Word Problems
Let’s solve the word problems we presented earlier.
Solution to Example 1: The Ladder Problem
We can use the Pythagorean theorem to find the distance from the base of the building to the point where Tom should place the ladder.
Let x be the distance from the base of the building to the point where Tom should place the ladder. We know that the ladder is 5 meters long, and the height of the building is 12 meters. We can use the Pythagorean theorem to write:
x² + 5² = 12²
Simplifying the equation, we get:
x² + 25 = 144
Subtracting 25 from both sides, we get:
x² = 119
Taking the square root of both sides, we get:
x = √119
Therefore, Tom should place the ladder approximately 10.95 meters from the base of the building.
Solution to Example 2: The Bridge Problem
We can use the Pythagorean theorem to find the width of the river.
Let x be the width of the river. We know that the length of the bridge is 30 meters, and the height of the bridge above the water is 10 meters. We can use the Pythagorean theorem to write:
x² + 10² = 30²
Simplifying the equation, we get:
x² + 100 = 900
Subtracting 100 from both sides, we get:
x² = 800
Taking the square root of both sides, we get:
x = √800
Therefore, the width of the river is approximately 28.28 meters.
Solution to Example 3: The Building Problem
We can use the Pythagorean theorem to find the length of the diagonal path.
Let x be the length of the diagonal path. We know that the length of the building is 20 meters, and the width is 15 meters. We can use the Pythagorean theorem to write:
x² = 20² + 15²
Simplifying the equation, we get:
x² = 400 + 225
Adding the numbers, we get:
x² = 625
Taking the square root of both sides, we get:
x = √625
Therefore, the length of the diagonal path is 25 meters.
Pythagorean Theorem Word Problems Worksheets
Here are some worksheets with word problems involving the Pythagorean theorem:
Worksheet 1: Basic Word Problems

| Problem | Answer |
|---|---|
| A rectangular garden measures 10 meters by 5 meters. What is the length of the diagonal path across the garden? | 11.18 meters |
| A right-angled triangle has one side that measures 8 meters and the other side measures 15 meters. What is the length of the hypotenuse? | 17 meters |
| A ladder leans against a wall, forming a right-angled triangle with the wall and the ground. The ladder is 6 meters long, and the distance from the base of the ladder to the wall is 8 meters. How high does the ladder reach? | 10 meters |
Worksheet 2: Real-World Applications
| Problem | Answer |
|---|---|
| A carpenter is building a roof that is 12 meters wide and 8 meters long. What is the length of the diagonal beam that spans the roof? | 14.42 meters |
| A bridge spans a river, and the length of the bridge is 40 meters. The height of the bridge above the water is 12 meters. How wide is the river? | 36.06 meters |
| A surveyor is measuring the distance between two points on a map. The distance between the points is 25 meters, and the angle between the points is 60 degrees. What is the length of the third side of the triangle? | 21.65 meters |
Conclusion
The Pythagorean theorem is a fundamental concept in geometry, and its applications are numerous in various fields. By using word problems to apply the Pythagorean theorem, we can see the practical value of this concept in real-world scenarios. We hope that the worksheets and solutions provided in this article will help you better understand the Pythagorean theorem and its applications.
What is the Pythagorean theorem?
+The Pythagorean theorem is a mathematical concept that describes the relationship between the lengths of the sides of a right-angled triangle. It states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
How do I use the Pythagorean theorem to solve word problems?
+To use the Pythagorean theorem to solve word problems, you need to identify the right-angled triangle in the problem and label the sides. Then, you can use the formula a² + b² = c² to solve for the unknown side.
What are some real-world applications of the Pythagorean theorem?
+The Pythagorean theorem has many real-world applications, including construction, physics, engineering, and architecture. It can be used to calculate distances, heights, and lengths in various scenarios.
Related Terms:
- Pythagorean Word Problems Worksheet pdf
- Pythagorean Theorem problems with answers