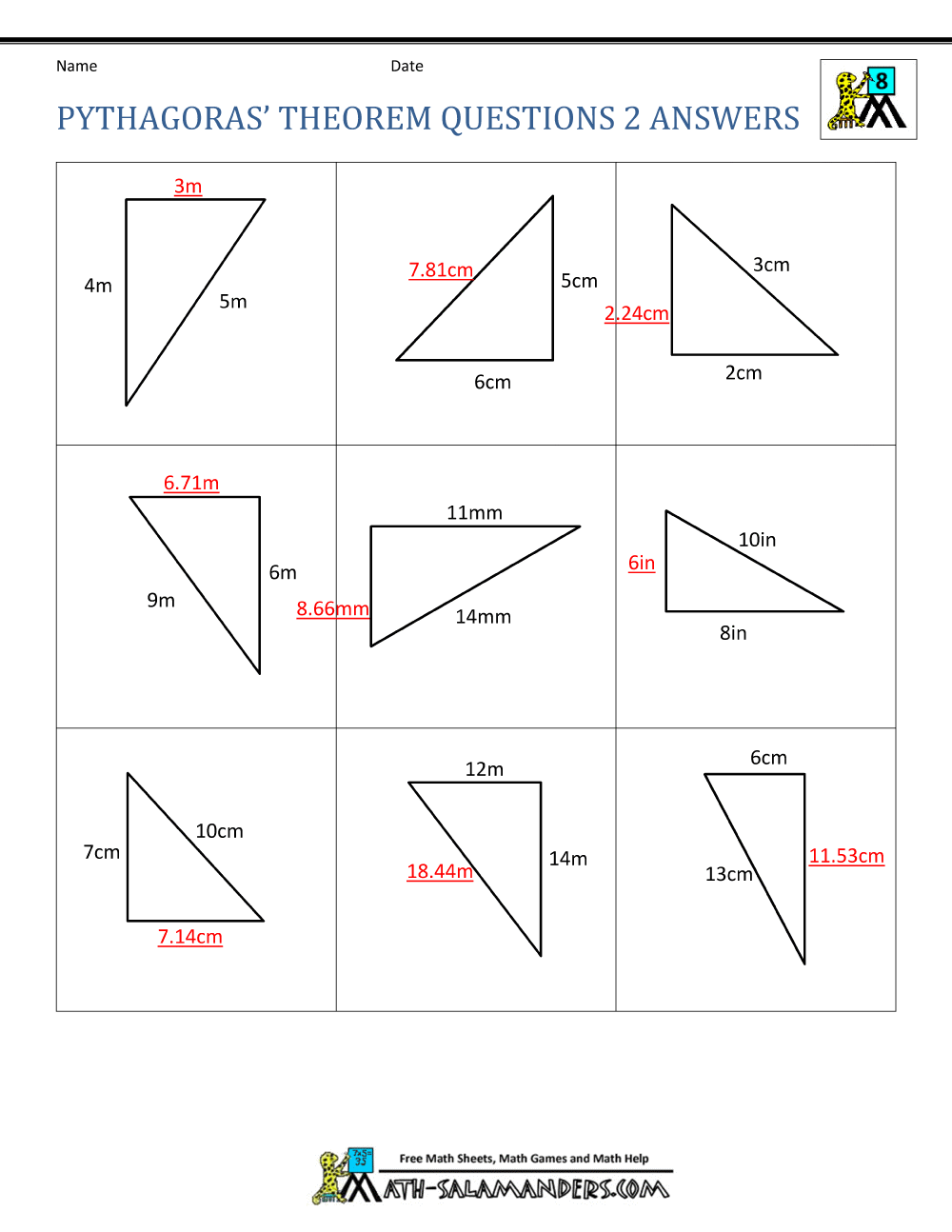
Pythagorean Theorem Worksheet With Answers and Solutions

Understanding the Pythagorean Theorem

The Pythagorean theorem is a fundamental concept in geometry and mathematics, describing the relationship between the lengths of the sides of a right-angled triangle. The theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This can be expressed mathematically as:

a² + b² = c²

where:

• a and b are the lengths of the two sides that form the right angle
• c is the length of the hypotenuse

Benefits of Using the Pythagorean Theorem

The Pythagorean theorem has numerous applications in various fields, including physics, engineering, architecture, and more. Some of the benefits of using the Pythagorean theorem include:

• Solving right-angled triangles: The theorem allows you to find the length of the hypotenuse or one of the other sides, given the lengths of the other two sides.
• Finding distances and heights: The theorem can be used to calculate distances and heights in real-world problems, such as determining the distance between two points on a map or the height of a building.
• Checking triangle properties: The theorem can be used to verify whether a triangle is a right-angled triangle or not.

Pythagorean Theorem Worksheet

Here’s a worksheet with 10 problems to help you practice using the Pythagorean theorem. Try to solve each problem on your own, and then check your answers with the solutions provided.

Problem 1

In a right-angled triangle, the length of the hypotenuse is 10 cm, and one of the other sides is 6 cm. Find the length of the third side.

Problem 2

A right-angled triangle has one side of length 8 cm and a hypotenuse of length 10 cm. Find the length of the other side.

Problem 3

In a right-angled triangle, the length of one side is 5 cm, and the length of the hypotenuse is 13 cm. Find the length of the other side.

Problem 4

A right-angled triangle has a hypotenuse of length 15 cm, and one of the other sides is 9 cm. Find the length of the third side.

Problem 5

In a right-angled triangle, the length of one side is 12 cm, and the length of the hypotenuse is 16 cm. Find the length of the other side.

Problem 6

A right-angled triangle has a hypotenuse of length 20 cm, and one of the other sides is 12 cm. Find the length of the third side.

Problem 7

In a right-angled triangle, the length of one side is 7 cm, and the length of the hypotenuse is 10 cm. Find the length of the other side.

Problem 8

A right-angled triangle has a hypotenuse of length 18 cm, and one of the other sides is 15 cm. Find the length of the third side.

Problem 9

In a right-angled triangle, the length of one side is 9 cm, and the length of the hypotenuse is 12 cm. Find the length of the other side.

Problem 10

A right-angled triangle has a hypotenuse of length 25 cm, and one of the other sides is 20 cm. Find the length of the third side.

Solutions

Problem 1

Using the Pythagorean theorem, we can find the length of the third side:

a² + b² = c² 6² + b² = 10² 36 + b² = 100 b² = 64 b = √64 = 8 cm

Problem 2

Using the Pythagorean theorem, we can find the length of the other side:

a² + b² = c² 8² + b² = 10² 64 + b² = 100 b² = 36 b = √36 = 6 cm

Problem 3

Using the Pythagorean theorem, we can find the length of the other side:

a² + b² = c² 5² + b² = 13² 25 + b² = 169 b² = 144 b = √144 = 12 cm

Problem 4

Using the Pythagorean theorem, we can find the length of the third side:

a² + b² = c² 9² + b² = 15² 81 + b² = 225 b² = 144 b = √144 = 12 cm

Problem 5

Using the Pythagorean theorem, we can find the length of the other side:

a² + b² = c² 12² + b² = 16² 144 + b² = 256 b² = 112 b = √112 = 4√7 cm

Problem 6

Using the Pythagorean theorem, we can find the length of the third side:

a² + b² = c² 12² + b² = 20² 144 + b² = 400 b² = 256 b = √256 = 16 cm

Problem 7

Using the Pythagorean theorem, we can find the length of the other side:

a² + b² = c² 7² + b² = 10² 49 + b² = 100 b² = 51 b = √51 cm

Problem 8

Using the Pythagorean theorem, we can find the length of the third side:

a² + b² = c² 15² + b² = 18² 225 + b² = 324 b² = 99 b = √99 = 3√11 cm

Problem 9

Using the Pythagorean theorem, we can find the length of the other side:

a² + b² = c² 9² + b² = 12² 81 + b² = 144 b² = 63 b = √63 = 3√7 cm

Problem 10

Using the Pythagorean theorem, we can find the length of the third side:

a² + b² = c² 20² + b² = 25² 400 + b² = 625 b² = 225 b = √225 = 15 cm

Notes

📝 Note: The Pythagorean theorem only applies to right-angled triangles.

📝 Note: The theorem can be used to find the length of the hypotenuse or one of the other sides, given the lengths of the other two sides.

Conclusion

The Pythagorean theorem is a powerful tool for solving right-angled triangles and finding distances and heights in various real-world problems. By understanding and applying the theorem, you can become more proficient in geometry and mathematics. Remember to practice regularly and use the theorem to solve different types of problems.