Pythagorean Theorem Word Problems Made Easy

Understanding the Pythagorean Theorem

The Pythagorean Theorem is a fundamental concept in geometry that has numerous applications in various fields, including physics, engineering, and architecture. It states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Mathematically, it can be expressed as:

a^2 + b^2 = c^2

where a and b are the lengths of the two sides, and c is the length of the hypotenuse.

Breaking Down the Formula

To better understand the Pythagorean Theorem, let’s break down the formula:

• a and b are the lengths of the two sides that form the right angle.
• c is the length of the hypotenuse, which is always the longest side of a right-angled triangle.
• ^2 means “squared,” which indicates that each side length is multiplied by itself.

Solving Word Problems with the Pythagorean Theorem

Now, let’s move on to some word problems that can be solved using the Pythagorean Theorem. These problems are designed to test your understanding of the concept and its applications.

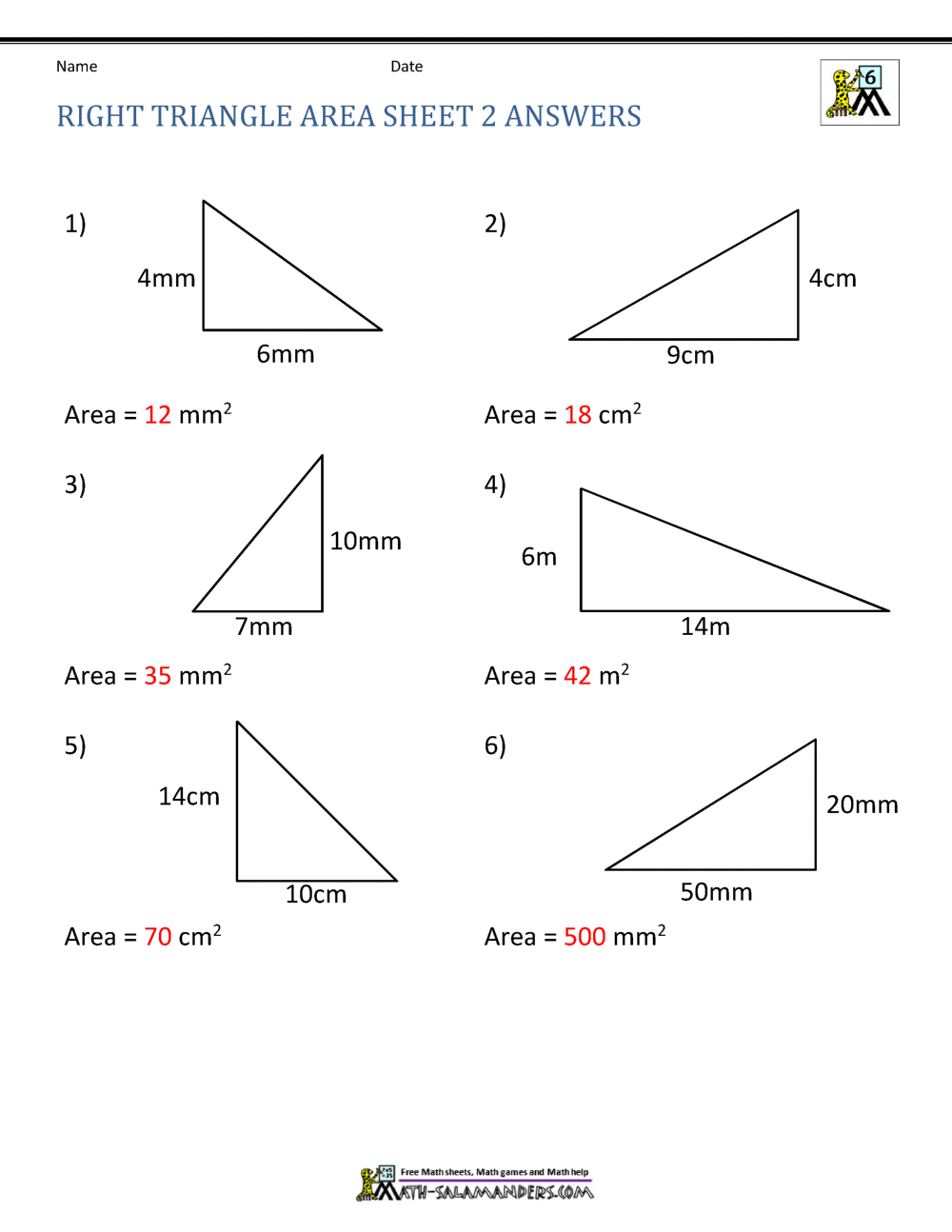
Problem 1: In a right-angled triangle, the length of one side is 3 inches, and the length of the other side is 4 inches. What is the length of the hypotenuse?

Solution: Using the Pythagorean Theorem, we can plug in the values of a and b:

3^2 + 4^2 = c^2 9 + 16 = c^2 25 = c^2

Taking the square root of both sides, we get:

c = √25 c = 5 inches

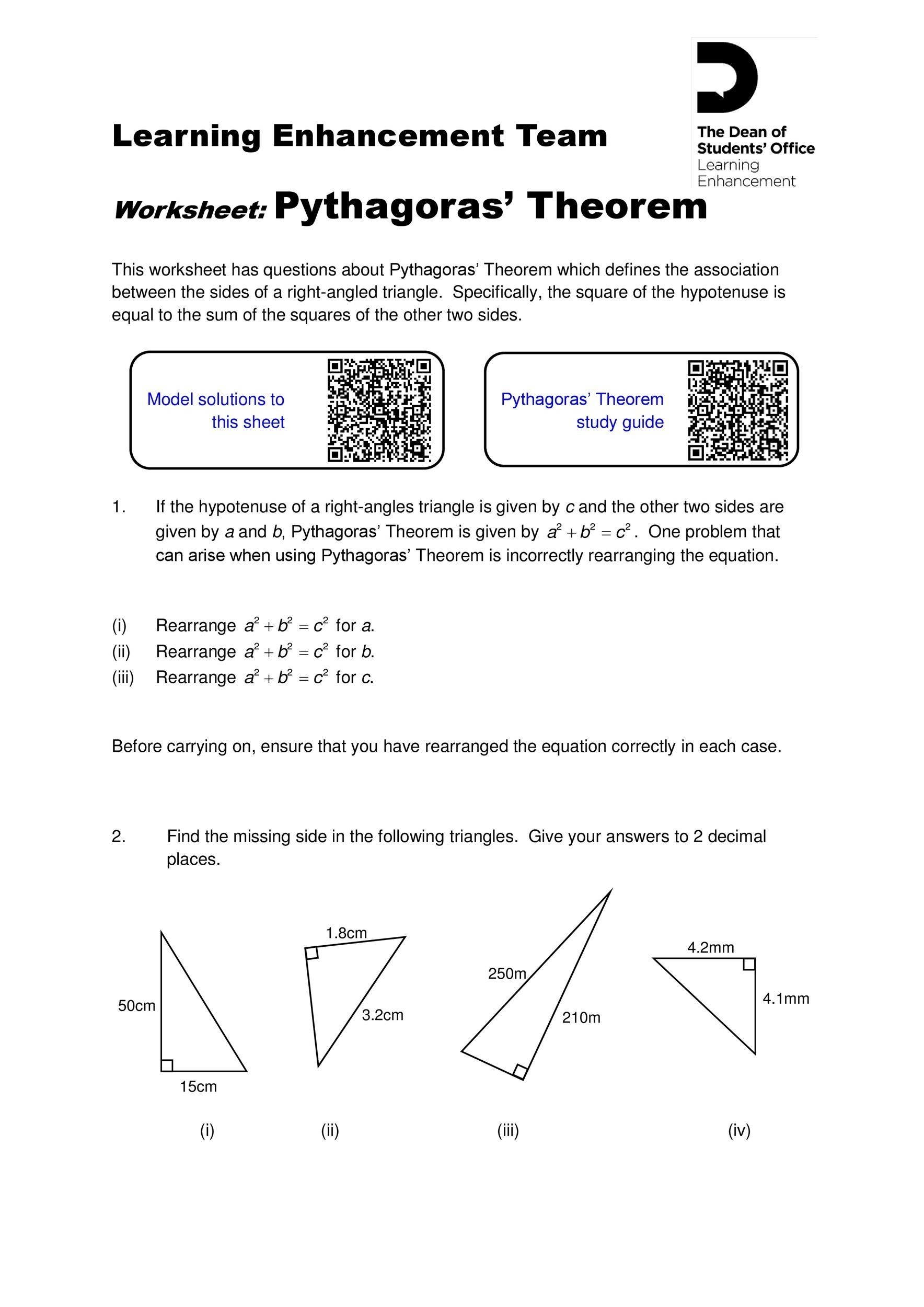
Problem 2: A ladder is leaning against a wall, forming a right-angled triangle. The length of the ladder is 10 feet, and the distance from the base of the ladder to the wall is 6 feet. How far up the wall does the ladder reach?

Solution: In this problem, the ladder is the hypotenuse ©, and the distance from the base of the ladder to the wall is one of the sides (a). We need to find the length of the other side (b), which is the height of the ladder against the wall.

Using the Pythagorean Theorem, we can plug in the values of a and c:

6^2 + b^2 = 10^2 36 + b^2 = 100

Subtracting 36 from both sides, we get:

b^2 = 64

Taking the square root of both sides, we get:

b = √64 b = 8 feet

Problem 3: A surveyor is measuring the distance between two points on a map. The distance between the two points is 12 kilometers, and the bearing (angle) between the two points is 60 degrees. What is the length of the side opposite the angle?

Solution: In this problem, we have a right-angled triangle with a known angle (60 degrees) and a known side length (12 kilometers). We need to find the length of the side opposite the angle.

First, we need to find the length of the adjacent side (a) using the cosine function:

cos(60°) = a / 12

Simplifying, we get:

a = 6 kilometers

Now, we can use the Pythagorean Theorem to find the length of the side opposite the angle (b):

6^2 + b^2 = 12^2 36 + b^2 = 144

Subtracting 36 from both sides, we get:

b^2 = 108

Taking the square root of both sides, we get:

b = √108 b ≈ 10.39 kilometers

💡 Note: In this problem, we used the cosine function to find the length of the adjacent side, and then used the Pythagorean Theorem to find the length of the side opposite the angle.

Common Pitfalls and Tips

When solving word problems with the Pythagorean Theorem, there are a few common pitfalls to watch out for:

• Make sure to read the problem carefully and identify the known values.
• Use the correct formula and plug in the correct values.
• Simplify the equation and solve for the unknown value.
• Check your units and make sure they are consistent.

Here are some additional tips to help you solve word problems with the Pythagorean Theorem:

• Draw a diagram to visualize the problem and identify the right-angled triangle.
• Use the Pythagorean Theorem to find the length of the hypotenuse or one of the sides.
• Check your work by plugging the values back into the formula.

Real-World Applications

The Pythagorean Theorem has numerous real-world applications in various fields, including:

• Physics: The Pythagorean Theorem is used to calculate distances and velocities in physics problems.
• Engineering: The Pythagorean Theorem is used to design buildings, bridges, and other structures.
• Architecture: The Pythagorean Theorem is used to design and construct buildings, including calculating the length of diagonals and the height of walls.

In conclusion, the Pythagorean Theorem is a powerful tool for solving word problems involving right-angled triangles. By understanding the formula and its applications, you can solve a wide range of problems in various fields. Remember to read the problem carefully, use the correct formula, and simplify the equation to solve for the unknown value.