5 Ways to Prove Triangles Congruent
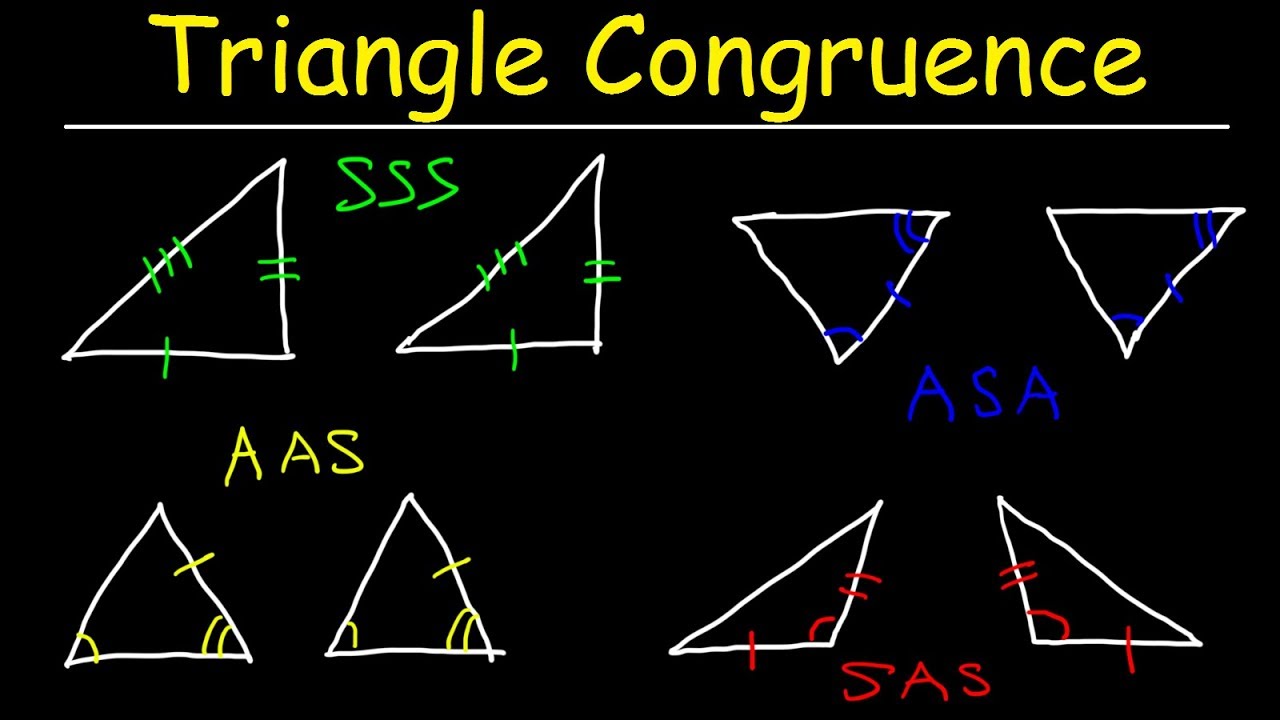
Understanding Triangle Congruence
In geometry, two triangles are said to be congruent if one can be transformed into the other through a combination of translations, rotations, and reflections. This means that the corresponding sides and angles of the two triangles are equal. Proving triangles congruent is a fundamental concept in geometry, and it has numerous applications in various fields such as architecture, engineering, and physics.
5 Ways to Prove Triangles Congruent
There are five common methods to prove triangles congruent:
1. Side-Side-Side (SSS) Congruence
If three sides of one triangle are equal to the corresponding three sides of another triangle, then the two triangles are congruent.
📝 Note: The order of the sides is not important. What matters is that the three sides of one triangle are equal to the three sides of the other triangle.
Example:

| Triangle ABC | Triangle DEF |
|---|---|
| AB = 5 cm | DE = 5 cm |
| BC = 6 cm | EF = 6 cm |
| AC = 7 cm | DF = 7 cm |
Since the three sides of triangle ABC are equal to the three sides of triangle DEF, the two triangles are congruent by SSS congruence.
2. Side-Angle-Side (SAS) Congruence
If two sides and the included angle of one triangle are equal to the corresponding two sides and included angle of another triangle, then the two triangles are congruent.
📝 Note: The included angle is the angle between the two equal sides.
Example:
| Triangle ABC | Triangle DEF |
|---|---|
| AB = 5 cm | DE = 5 cm |
| ∠B = 60° | ∠E = 60° |
| BC = 6 cm | EF = 6 cm |
Since the two sides and included angle of triangle ABC are equal to the two sides and included angle of triangle DEF, the two triangles are congruent by SAS congruence.
3. Angle-Side-Angle (ASA) Congruence
If two angles and the included side of one triangle are equal to the corresponding two angles and included side of another triangle, then the two triangles are congruent.
📝 Note: The included side is the side between the two equal angles.
Example:
| Triangle ABC | Triangle DEF |
|---|---|
| ∠A = 30° | ∠D = 30° |
| AB = 5 cm | DE = 5 cm |
| ∠C = 60° | ∠F = 60° |
Since the two angles and included side of triangle ABC are equal to the two angles and included side of triangle DEF, the two triangles are congruent by ASA congruence.
4. Angle-Angle-Side (AAS) Congruence
If two angles and a non-included side of one triangle are equal to the corresponding two angles and non-included side of another triangle, then the two triangles are congruent.
📝 Note: The non-included side is the side that is not between the two equal angles.
Example:
| Triangle ABC | Triangle DEF |
|---|---|
| ∠A = 30° | ∠D = 30° |
| ∠C = 60° | ∠F = 60° |
| BC = 6 cm | EF = 6 cm |
Since the two angles and non-included side of triangle ABC are equal to the two angles and non-included side of triangle DEF, the two triangles are congruent by AAS congruence.
5. Hypotenuse-Leg (HL) Congruence
If the hypotenuse and a leg of one right triangle are equal to the corresponding hypotenuse and leg of another right triangle, then the two triangles are congruent.
📝 Note: This method only applies to right triangles.
Example:
| Triangle ABC | Triangle DEF |
|---|---|
| AB = 5 cm (hypotenuse) | DE = 5 cm (hypotenuse) |
| BC = 6 cm (leg) | EF = 6 cm (leg) |
Since the hypotenuse and leg of triangle ABC are equal to the hypotenuse and leg of triangle DEF, the two triangles are congruent by HL congruence.
In conclusion, these five methods provide a comprehensive approach to proving triangles congruent. By understanding and applying these methods, one can determine whether two triangles are congruent, which is essential in various mathematical and real-world applications.
What is the difference between SSS and SAS congruence?
+
SSS congruence involves three equal sides, while SAS congruence involves two equal sides and the included angle.
Can ASA congruence be applied to right triangles?
+
No, ASA congruence is not applicable to right triangles. Instead, HL congruence is used for right triangles.
What is the significance of proving triangles congruent?
+
Proving triangles congruent is essential in various mathematical and real-world applications, such as architecture, engineering, and physics, as it allows for the comparison and analysis of geometric shapes.



