Proving Lines Parallel Worksheet Made Easy

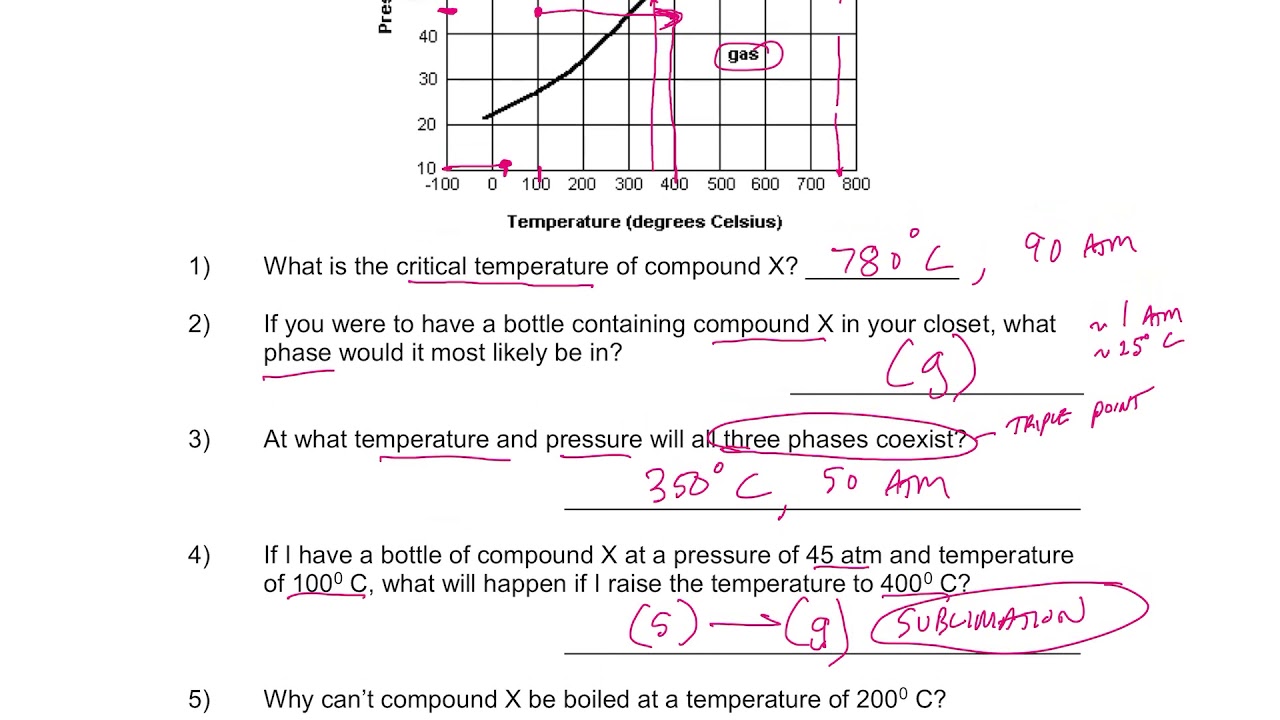
Mastering Parallel Lines: A Comprehensive Guide
Parallel lines are a fundamental concept in geometry, and understanding how to prove them is crucial for various mathematical applications. In this post, we will delve into the world of parallel lines, exploring the different methods to prove their existence. Whether you’re a student, teacher, or simply a math enthusiast, this guide will provide you with a thorough understanding of parallel lines and help you become proficient in proving them.
Understanding Parallel Lines
Before diving into the methods of proving parallel lines, it’s essential to understand the definition and properties of parallel lines. Parallel lines are two lines that lie in the same plane and never intersect, no matter how far they are extended. In other words, parallel lines have the same slope and are always equidistant from each other.
Methods to Prove Parallel Lines
There are several methods to prove parallel lines, including:
- Corresponding Angles Theorem: If two lines are cut by a transversal and the corresponding angles are congruent, then the lines are parallel.
- Alternate Interior Angles Theorem: If two lines are cut by a transversal and the alternate interior angles are congruent, then the lines are parallel.
- Alternate Exterior Angles Theorem: If two lines are cut by a transversal and the alternate exterior angles are congruent, then the lines are parallel.
- Consecutive Interior Angles Theorem: If two lines are cut by a transversal and the consecutive interior angles are supplementary, then the lines are parallel.
📝 Note: These theorems can be applied to prove parallel lines in various scenarios, including when a transversal intersects two lines, or when two lines are intersected by a third line.
Examples and Practice Problems
To reinforce your understanding of parallel lines, let’s explore some examples and practice problems:
Example 1: Prove that the lines AB and CD are parallel.
Given: AB and CD are cut by a transversal EF
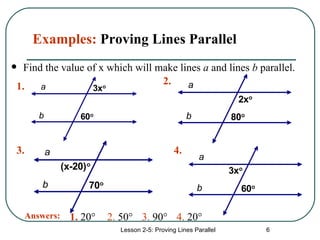
| Angle 1 | Angle 2 | Angle 3 | Angle 4 | |
|---|---|---|---|---|
| Measures | 30° | 150° | 30° | 150° |
Solution: Using the Corresponding Angles Theorem, we can see that the corresponding angles (1 and 3, 2 and 4) are congruent. Therefore, AB and CD are parallel.
Practice Problem 1: Prove that the lines GH and IJ are parallel.
Given: GH and IJ are cut by a transversal KL
| Angle 1 | Angle 2 | Angle 3 | Angle 4 | |
|---|---|---|---|---|
| Measures | 45° | 135° | 45° | 135° |
📝 Note: Use the Alternate Interior Angles Theorem to prove the parallelism of `GH` and `IJ`.
Conclusion
Proving parallel lines is a fundamental skill in geometry, and with practice and patience, you can become proficient in applying the various methods. Remember to use the theorems and properties of parallel lines to prove their existence, and don’t hesitate to seek help when needed.
What is the definition of parallel lines?
+Parallel lines are two lines that lie in the same plane and never intersect, no matter how far they are extended.
What are the methods to prove parallel lines?
+The methods to prove parallel lines include the Corresponding Angles Theorem, Alternate Interior Angles Theorem, Alternate Exterior Angles Theorem, and Consecutive Interior Angles Theorem.
How can I practice proving parallel lines?
+You can practice proving parallel lines by working on practice problems and using online resources, such as worksheets and video tutorials.