5 Essential Probability Concepts to Master

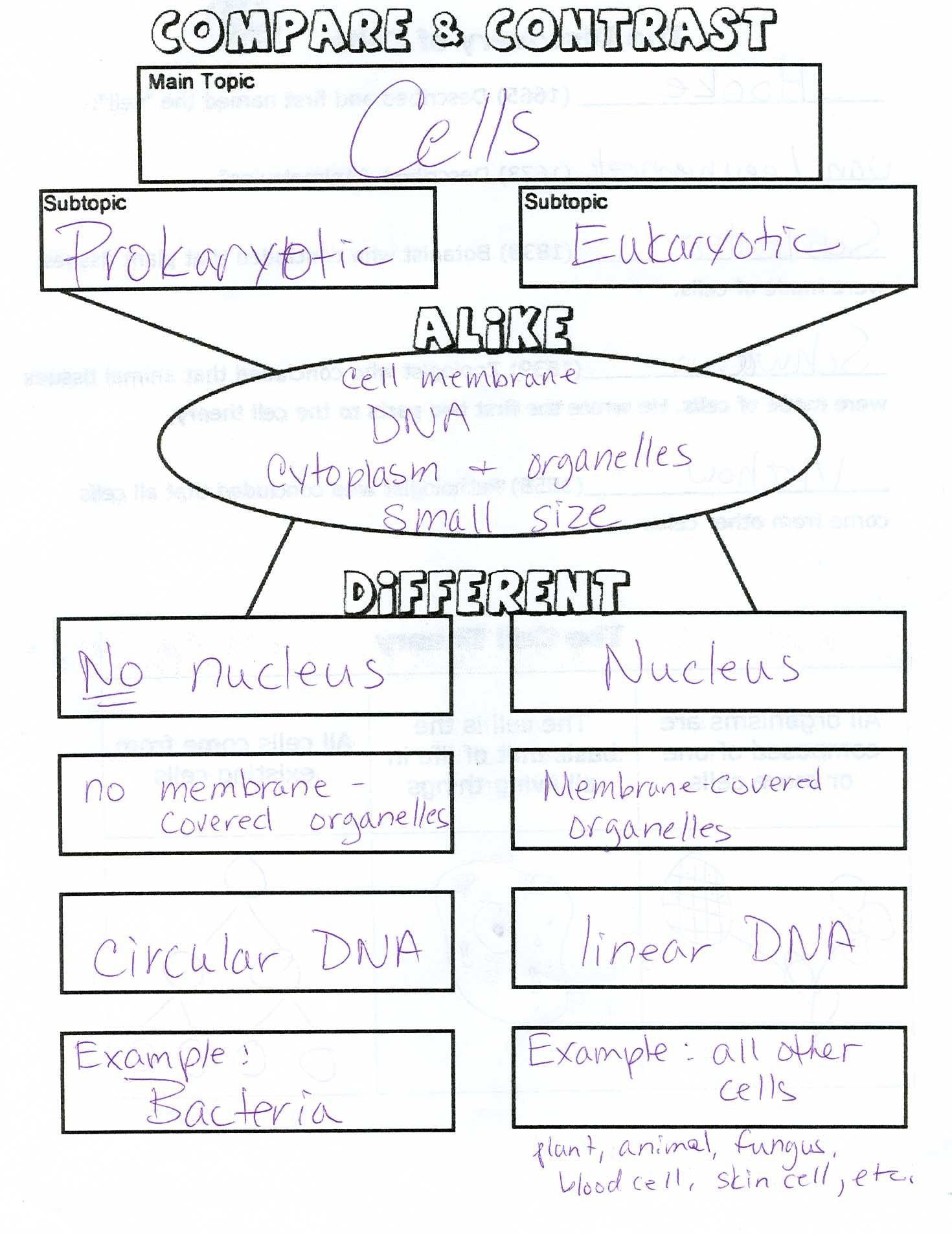
Understanding Probability: A Foundational Knowledge
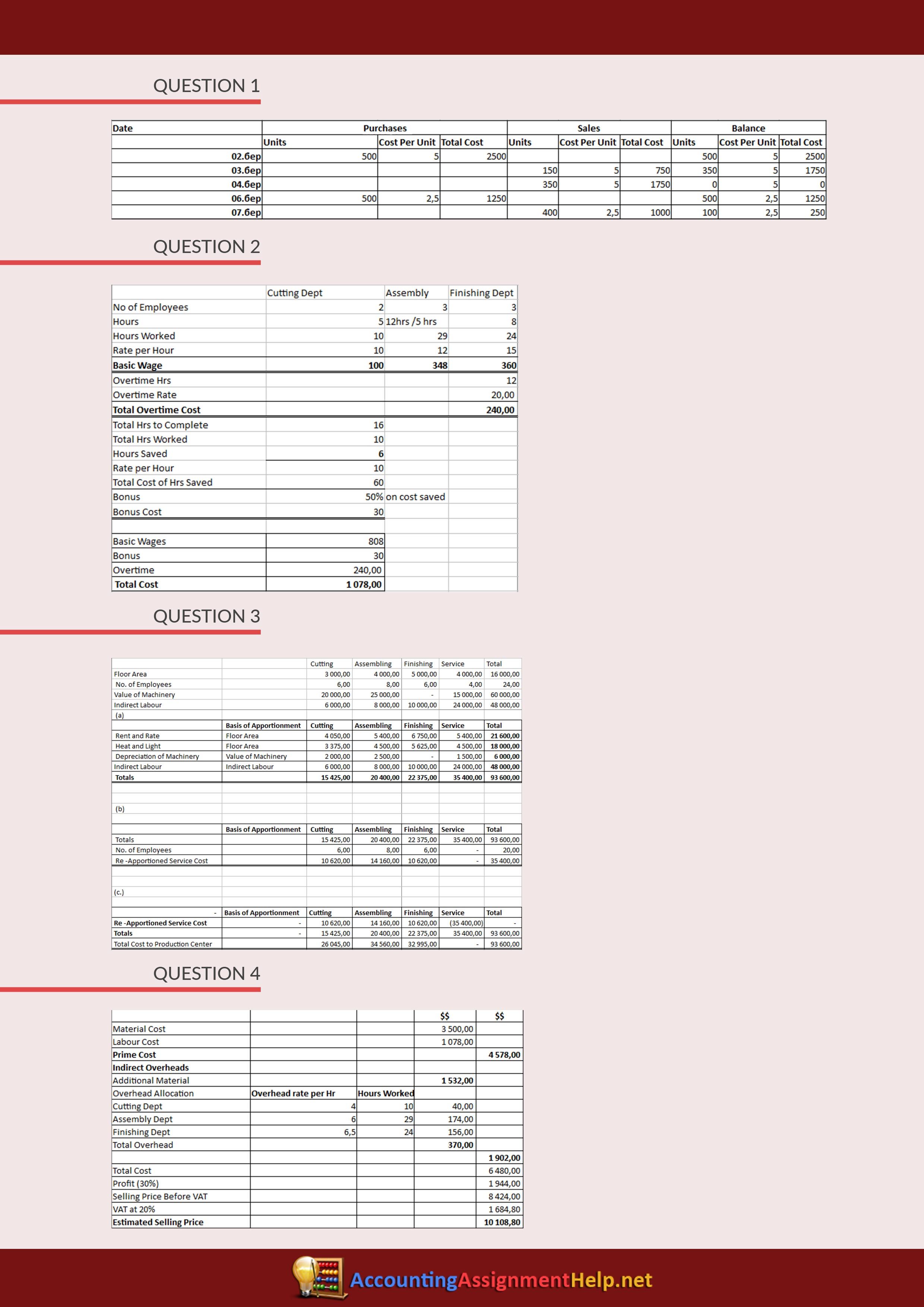
Probability is a fundamental concept in mathematics and statistics, and it has numerous applications in various fields, including science, engineering, economics, and finance. Mastering probability concepts is essential for making informed decisions, predicting outcomes, and analyzing data. In this article, we will explore five essential probability concepts that you need to understand to improve your analytical skills and make better decisions.
1. Basic Probability Definition
Probability is a measure of the likelihood of an event occurring. It is defined as the number of favorable outcomes divided by the total number of possible outcomes. The probability of an event is always between 0 and 1, where 0 indicates an impossible event and 1 indicates a certain event.
Formula:
P(A) = Number of favorable outcomes / Total number of possible outcomes
2. Independent and Dependent Events
In probability, events can be classified into two categories: independent and dependent events.
- Independent Events: These are events where the occurrence of one event does not affect the probability of the other event. For example, flipping two coins is an independent event, as the outcome of one coin does not affect the outcome of the other coin.
- Dependent Events: These are events where the occurrence of one event affects the probability of the other event. For example, drawing two cards from a deck is a dependent event, as the first card drawn affects the probability of the second card.
3. Conditional Probability
Conditional probability is the probability of an event occurring given that another event has occurred. It is calculated using the formula:
P(A|B) = P(A ∩ B) / P(B)
where P(A|B) is the conditional probability of event A given event B, P(A ∩ B) is the probability of both events A and B occurring, and P(B) is the probability of event B occurring.
4. Bayes' Theorem
Bayes’ theorem is a fundamental concept in probability theory that describes the probability of an event based on prior knowledge and new evidence. It is calculated using the formula:
P(A|B) = P(B|A) * P(A) / P(B)
where P(A|B) is the posterior probability of event A given event B, P(B|A) is the likelihood of event B given event A, P(A) is the prior probability of event A, and P(B) is the prior probability of event B.
5. Expected Value
Expected value is a measure of the average outcome of an event. It is calculated by multiplying each possible outcome by its probability and summing the results.
E(X) = ∑xP(x)
where E(X) is the expected value, x is the outcome, and P(x) is the probability of the outcome.
📝 Note: Mastering these five essential probability concepts will help you to better understand and analyze data, make informed decisions, and predict outcomes. However, it is essential to practice and apply these concepts to real-world problems to reinforce your understanding.
In conclusion, probability is a vital concept in mathematics and statistics, and mastering its essential concepts is crucial for making informed decisions and analyzing data. By understanding basic probability definition, independent and dependent events, conditional probability, Bayes’ theorem, and expected value, you will be able to improve your analytical skills and make better decisions.
What is the difference between independent and dependent events?
+Independent events are events where the occurrence of one event does not affect the probability of the other event. Dependent events are events where the occurrence of one event affects the probability of the other event.
How is conditional probability calculated?
+Conditional probability is calculated using the formula P(A|B) = P(A ∩ B) / P(B), where P(A|B) is the conditional probability of event A given event B, P(A ∩ B) is the probability of both events A and B occurring, and P(B) is the probability of event B occurring.
What is the purpose of Bayes’ theorem?
+Bayes’ theorem is used to update the probability of an event based on prior knowledge and new evidence. It is calculated using the formula P(A|B) = P(B|A) * P(A) / P(B), where P(A|B) is the posterior probability of event A given event B, P(B|A) is the likelihood of event B given event A, P(A) is the prior probability of event A, and P(B) is the prior probability of event B.
Related Terms:
- Probability Review Worksheet PDF
- Probability Worksheet with answers PDF
- Basic probability worksheet PDF
- Algebra 2 probability test pdf
- Experimental probability Worksheet PDF