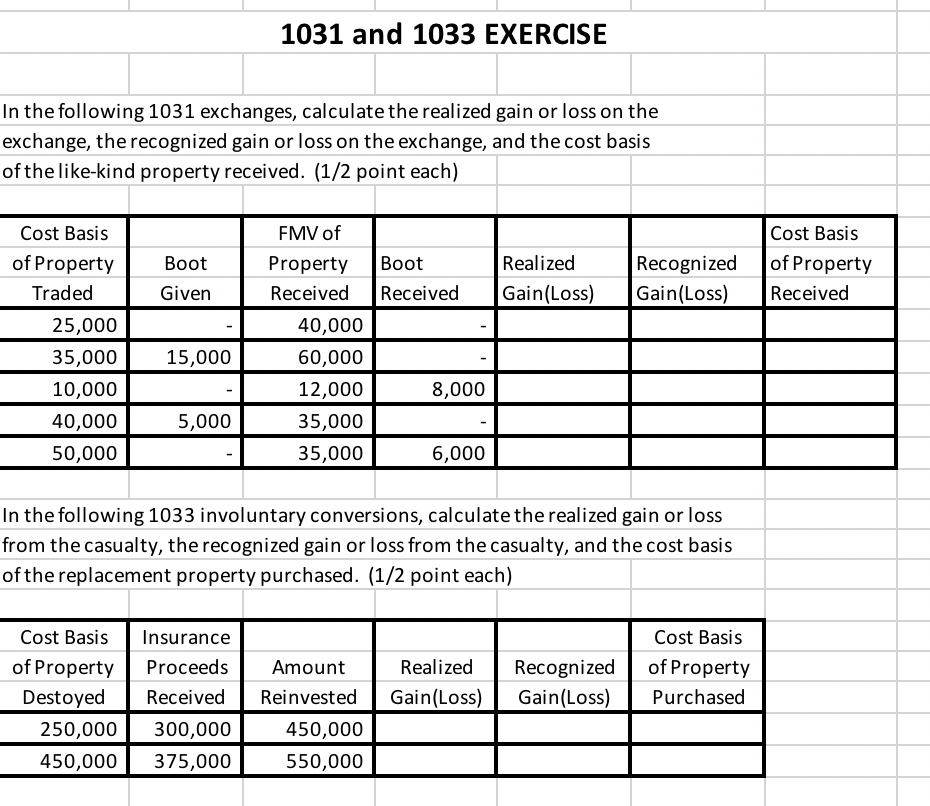
5 Ways to Master Prime Factorization

Mastering Prime Factorization: A Key to Unlocking Math Problems

Prime factorization is a fundamental concept in mathematics that involves breaking down a composite number into its prime factors. It is a crucial skill to master, as it has numerous applications in various areas of mathematics, such as algebra, geometry, and number theory. In this article, we will explore five ways to master prime factorization, along with some tips and tricks to help you become proficient in this skill.

Understanding the Concept of Prime Factorization

Before we dive into the methods, let’s quickly review the concept of prime factorization. Prime factorization is the process of expressing a composite number as a product of prime numbers. For example, the prime factorization of 12 is 2 × 2 × 3, since 2 and 3 are prime numbers. A composite number can have multiple prime factorizations, but the most efficient way is to use the prime factorization with the smallest prime factors.

Method 1: Division Method

The division method is a simple and straightforward way to find the prime factorization of a number. Here’s how it works:

• Divide the number by the smallest prime number, which is 2.
• If the number is divisible by 2, divide it by 2 again and again until it is no longer divisible.
• Move on to the next prime number, which is 3, and repeat the process.
• Continue this process until the number is reduced to 1.

For example, let’s find the prime factorization of 24 using the division method:

24 ÷ 2 = 12 12 ÷ 2 = 6 6 ÷ 2 = 3 3 ÷ 3 = 1

Therefore, the prime factorization of 24 is 2 × 2 × 2 × 3.

🤔 Note: This method can be time-consuming for larger numbers, so it's essential to use it in combination with other methods.

Method 2: Factor Tree Method

The factor tree method is a visual approach to finding the prime factorization of a number. Here’s how it works:

• Start with the number and find two factors that multiply to give the number.
• Draw a tree with the number at the top and the two factors as branches.
• Repeat the process for each factor, finding two factors that multiply to give the factor.
• Continue this process until the factors are prime numbers.

For example, let’s find the prime factorization of 36 using the factor tree method:

36 |
6 6 | \ |
2 3 2 3

Therefore, the prime factorization of 36 is 2 × 2 × 3 × 3.

Method 3: Using a Prime Factorization Chart

A prime factorization chart is a table that shows the prime factors of numbers up to a certain value. Here’s how to use it:

• Find the number in the chart and look for the prime factors listed next to it.
• Write down the prime factors and their corresponding exponents.

For example, let’s find the prime factorization of 48 using a prime factorization chart:

Therefore, the prime factorization of 48 is 2^4 × 3.

Method 4: Using a Calculator or Online Tool

There are many online tools and calculators available that can find the prime factorization of a number for you. Here’s how to use them:

• Enter the number into the calculator or online tool.
• Press the “prime factorization” button or select the “prime factorization” option.
• The tool will display the prime factors and their corresponding exponents.

For example, let’s find the prime factorization of 60 using an online tool:

60 = 2 × 2 × 3 × 5

Method 5: Practice and Memorization

The final method is to practice and memorize the prime factorization of numbers. Here’s how to do it:

• Start with small numbers and find their prime factorizations using one of the above methods.
• Practice regularly and try to memorize the prime factorizations of numbers up to a certain value.
• Use flashcards or create a chart to help you memorize the prime factorizations.

For example, let’s memorize the prime factorization of numbers up to 100:

2 = 2 3 = 3 4 = 2 × 2 5 = 5 6 = 2 × 3 7 = 7 8 = 2 × 2 × 2 9 = 3 × 3 10 = 2 × 5

By mastering prime factorization, you can unlock a range of math problems and develop a deeper understanding of number theory. With these five methods, you can become proficient in prime factorization and take your math skills to the next level.