Mastering Piecewise Functions with Our Free Worksheet
Understanding Piecewise Functions
Piecewise functions are a fundamental concept in mathematics, particularly in algebra and calculus. They are used to describe a function that has different definitions for different intervals of the input variable. In this article, we will delve into the world of piecewise functions, exploring their definition, notation, and applications. We will also provide a free worksheet to help you master these functions.
What is a Piecewise Function?
A piecewise function is a function that is defined by multiple sub-functions, each applied to a specific interval of the input variable. The function “pieces” together these sub-functions to create a new function that is defined for all input values. Piecewise functions are often used to model real-world phenomena that have different behaviors or patterns over different intervals.
Notation and Definition
Piecewise functions are typically denoted using the following notation:
f(x) = { f1(x) if x ∈ D1, f2(x) if x ∈ D2, … fn(x) if x ∈ Dn }
where f(x) is the piecewise function, f1(x), f2(x),…, fn(x) are the sub-functions, and D1, D2,…, Dn are the intervals over which each sub-function is defined.
For example, consider the piecewise function:
f(x) = { x^2 if x ≥ 0, -x^2 if x < 0 }
This function is defined as x^2 for all non-negative values of x and -x^2 for all negative values of x.
Types of Piecewise Functions
There are several types of piecewise functions, including:
- Continuous piecewise functions: These functions are continuous at all points, meaning that the sub-functions “meet” at the endpoints of each interval.
- Discontinuous piecewise functions: These functions are discontinuous at one or more points, meaning that the sub-functions do not “meet” at the endpoints of each interval.
- Piecewise linear functions: These functions are composed of linear sub-functions that are “pieced together” to form a new function.
Applications of Piecewise Functions
Piecewise functions have numerous applications in various fields, including:
- Physics: Piecewise functions are used to model the motion of objects that change direction or speed at certain points.
- Economics: Piecewise functions are used to model the behavior of consumers and producers in different market conditions.
- Computer Science: Piecewise functions are used in algorithms and data structures to model complex systems.
How to Graph Piecewise Functions
Graphing piecewise functions involves graphing each sub-function over its respective interval and then “piecing together” the graphs. Here are the steps to graph a piecewise function:
- Identify the intervals over which each sub-function is defined.
- Graph each sub-function over its respective interval.
- “Piece together” the graphs to form the complete graph of the piecewise function.
📝 Note: When graphing a piecewise function, it's essential to indicate the intervals over which each sub-function is defined.
Common Mistakes to Avoid
When working with piecewise functions, it’s essential to avoid the following common mistakes:
- Forgetting to indicate the intervals: Failing to specify the intervals over which each sub-function is defined can lead to confusion and errors.
- Incorrectly graphing the sub-functions: Graphing the sub-functions incorrectly can result in an inaccurate graph of the piecewise function.
- Failing to check for continuity: Failing to check if the piecewise function is continuous at all points can lead to incorrect conclusions.
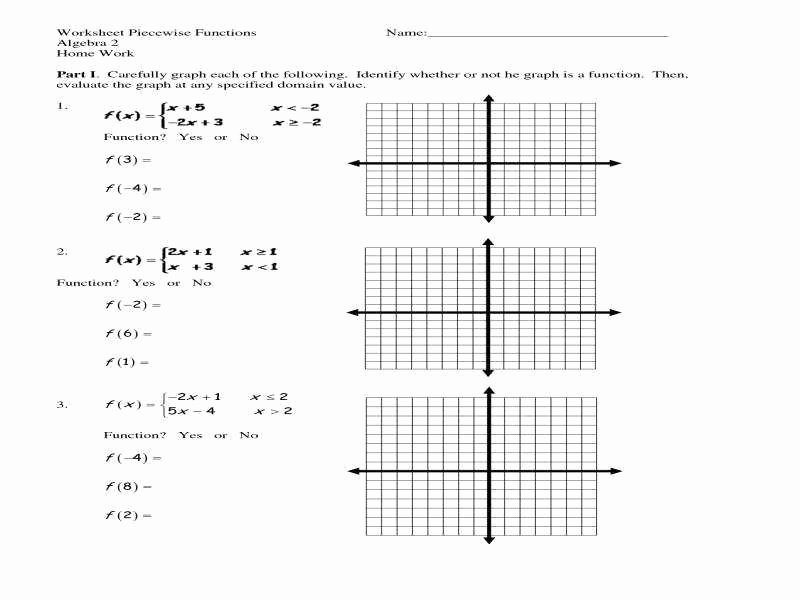
Free Worksheet
To help you master piecewise functions, we’ve created a free worksheet that includes exercises and examples. Download the worksheet below to test your understanding of piecewise functions.
[Insert image of worksheet]
Conclusion
In conclusion, piecewise functions are a powerful tool for modeling complex systems and phenomena. By understanding the definition, notation, and applications of piecewise functions, you can become proficient in working with these functions. Remember to avoid common mistakes and use our free worksheet to practice and reinforce your understanding.
What is a piecewise function?
+A piecewise function is a function that is defined by multiple sub-functions, each applied to a specific interval of the input variable.
How do I graph a piecewise function?
+To graph a piecewise function, identify the intervals over which each sub-function is defined, graph each sub-function over its respective interval, and then “piece together” the graphs to form the complete graph of the piecewise function.
What are some common mistakes to avoid when working with piecewise functions?
+Common mistakes to avoid include forgetting to indicate the intervals, incorrectly graphing the sub-functions, and failing to check for continuity.