Piecewise Function Worksheet Answers
Understanding Piecewise Functions
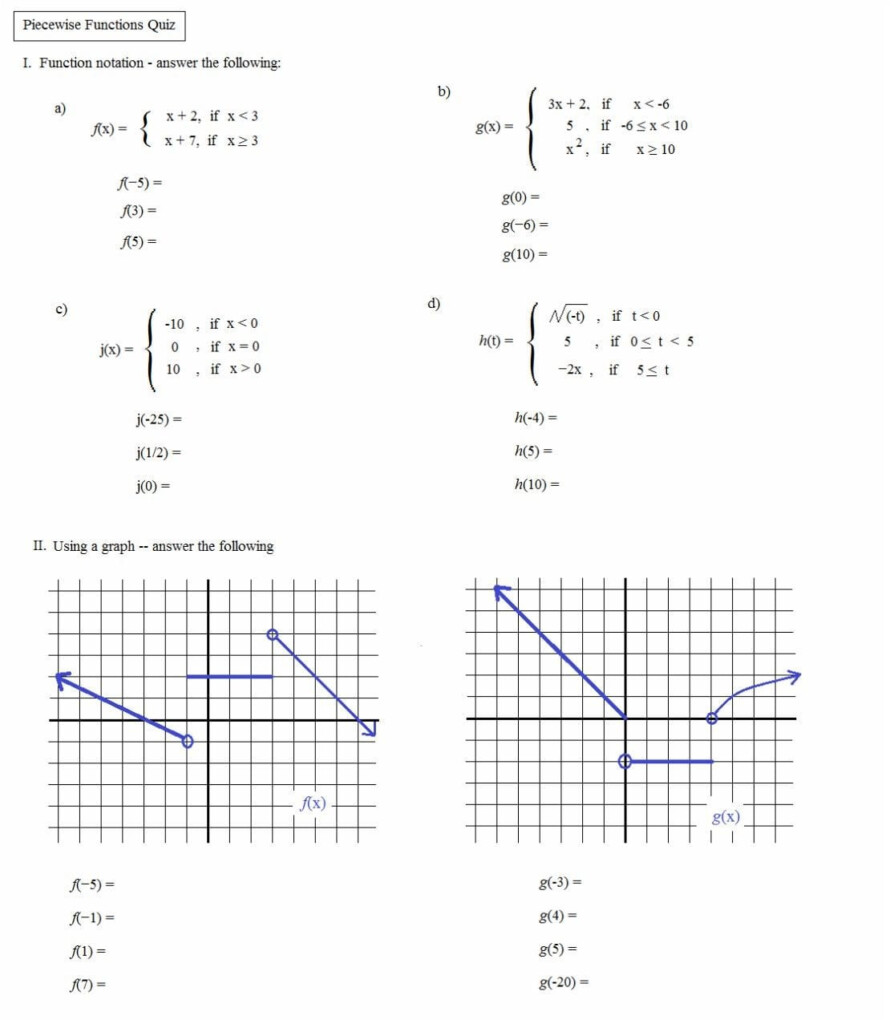
A piecewise function is a function that is defined by multiple sub-functions, each applied to a specific interval of the domain. In this worksheet, we will explore the concept of piecewise functions and provide answers to common problems.
What is a Piecewise Function?
A piecewise function is a function that is defined by multiple sub-functions, each applied to a specific interval of the domain. The function is typically written in the following format:
f(x) = { sub-function 1, if x is in interval 1 sub-function 2, if x is in interval 2 … sub-function n, if x is in interval n }
For example:
f(x) = { x^2, if x >= 0 x + 1, if x < 0 }
In this example, the function f(x) is defined as x^2 for x greater than or equal to 0, and x + 1 for x less than 0.
Evaluating Piecewise Functions
To evaluate a piecewise function, we need to determine which sub-function to apply based on the value of x. We do this by checking which interval x falls into.
For example, suppose we want to evaluate the function f(x) = { x^2, if x >= 0; x + 1, if x < 0 } at x = 2.
Since x = 2 falls into the interval x >= 0, we apply the sub-function x^2:
f(2) = 2^2 = 4
On the other hand, if we want to evaluate the function at x = -1, we apply the sub-function x + 1:
f(-1) = -1 + 1 = 0
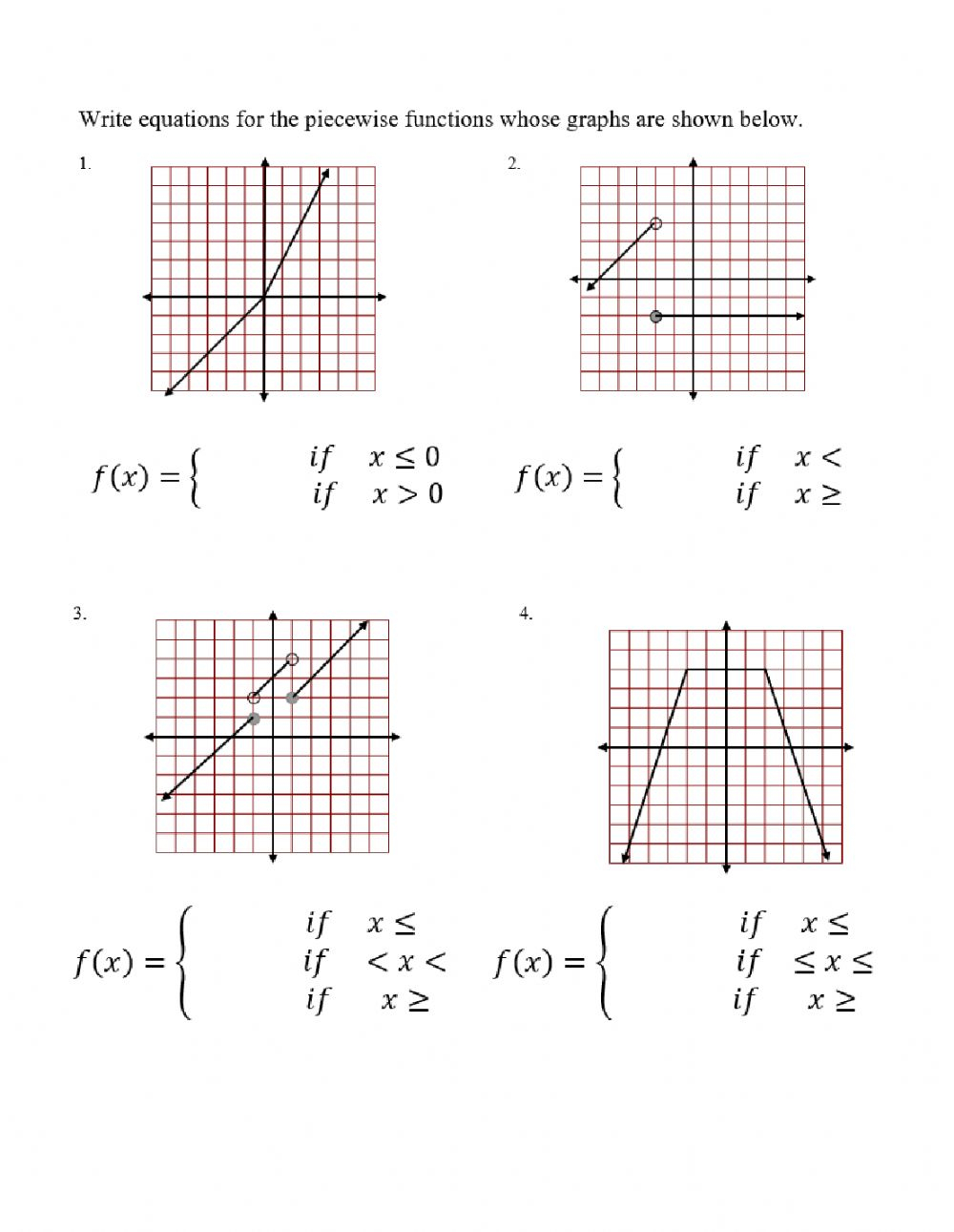
Graphing Piecewise Functions
Graphing a piecewise function involves graphing each sub-function separately and then combining the graphs.
For example, suppose we want to graph the function f(x) = { x^2, if x >= 0; x + 1, if x < 0 }.
We start by graphing the sub-function x^2 for x >= 0:
| x | y |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
Next, we graph the sub-function x + 1 for x < 0:
| x | y |
|---|---|
| -1 | 0 |
| -2 | -1 |
| -3 | -2 |
Finally, we combine the two graphs to get the graph of the piecewise function:
📝 Note: When graphing a piecewise function, we need to make sure that the graph is continuous at the breakpoints. In this example, the graph is continuous at x = 0.
Common Piecewise Functions
Some common piecewise functions include:
- Absolute value function: f(x) = |x| = { x, if x >= 0; -x, if x < 0 }
- Step function: f(x) = { 0, if x < 0; 1, if x >= 0 }
- Signum function: f(x) = { 1, if x > 0; 0, if x = 0; -1, if x < 0 }
Conclusion
In this worksheet, we have explored the concept of piecewise functions and provided answers to common problems. We have also graphed piecewise functions and discussed common piecewise functions.
When working with piecewise functions, it is essential to determine which sub-function to apply based on the value of x. We can then evaluate the function, graph the function, and analyze the results.
What is a piecewise function?
+A piecewise function is a function that is defined by multiple sub-functions, each applied to a specific interval of the domain.
How do you evaluate a piecewise function?
+To evaluate a piecewise function, we need to determine which sub-function to apply based on the value of x. We do this by checking which interval x falls into.
What is the graph of a piecewise function?
+The graph of a piecewise function is the combination of the graphs of each sub-function. We need to make sure that the graph is continuous at the breakpoints.
Related Terms:
- Piecewise function Worksheet pdf
- Algebra 2 piecewise Functions Worksheet
- Evaluating piecewise Functions worksheet
- Graphing piecewise functions worksheet
- Amr piecewise Functions answer Key