Parent Functions Worksheet

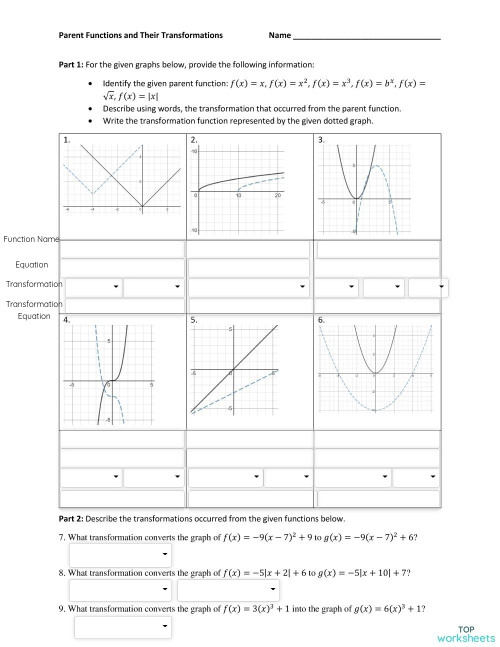
Parent functions are the most basic functions in mathematics, and they are used to build more complex functions. Understanding parent functions is essential for success in algebra and other areas of mathematics. In this worksheet, we will explore the different types of parent functions, their graphs, and how to identify and manipulate them.

Types of Parent Functions

There are several types of parent functions, including:

• Linear Functions: A linear function is a function whose graph is a straight line. The general form of a linear function is f(x) = mx + b, where m is the slope and b is the y-intercept.
• Quadratic Functions: A quadratic function is a function whose graph is a parabola. The general form of a quadratic function is f(x) = ax^2 + bx + c, where a, b, and c are constants.
• Polynomial Functions: A polynomial function is a function whose graph is a curve. The general form of a polynomial function is f(x) = anx^n + a(n-1)x^(n-1) +… + a_1x + a_0, where an, a(n-1),…, a_1, and a_0 are constants.
• Rational Functions: A rational function is a function whose graph is a curve. The general form of a rational function is f(x) = p(x) / q(x), where p(x) and q(x) are polynomial functions.
• Exponential Functions: An exponential function is a function whose graph is a curve that increases or decreases rapidly. The general form of an exponential function is f(x) = a^x, where a is a constant.
• Logarithmic Functions: A logarithmic function is a function whose graph is a curve that increases or decreases slowly. The general form of a logarithmic function is f(x) = log_a(x), where a is a constant.

Graphs of Parent Functions

Each parent function has a unique graph that can be used to identify it. Here are the graphs of some common parent functions:

• Linear Function:
• Quadratic Function:
• Polynomial Function:
• Rational Function:
• Exponential Function:
• Logarithmic Function:

Identifying Parent Functions

To identify a parent function, you need to look at its graph and determine the type of function it represents. Here are some tips for identifying parent functions:

• Look for symmetry: If the graph is symmetric about the y-axis, it may be a quadratic or polynomial function. If the graph is symmetric about the x-axis, it may be a rational or logarithmic function.
• Look for asymptotes: If the graph has asymptotes, it may be a rational or logarithmic function.
• Look for intervals of increase and decrease: If the graph is increasing or decreasing over certain intervals, it may be an exponential or logarithmic function.

Manipulating Parent Functions

Parent functions can be manipulated by adding, subtracting, multiplying, or dividing by constants. Here are some examples of how to manipulate parent functions:

• Adding or subtracting a constant: f(x) = x^2 + 3 is a quadratic function that has been shifted up by 3 units.
• Multiplying or dividing by a constant: f(x) = 2x^2 is a quadratic function that has been stretched vertically by a factor of 2.

📝 Note: When manipulating parent functions, it's essential to remember that the graph of the function will change accordingly.

Exercise

Identify the type of parent function represented by the graph below:

A) Linear Function B) Quadratic Function C) Polynomial Function D) Rational Function E) Exponential Function F) Logarithmic Function

Answer: B) Quadratic Function

Conclusion

Parent functions are the building blocks of mathematics, and understanding them is essential for success in algebra and other areas of mathematics. By identifying and manipulating parent functions, you can build more complex functions and solve real-world problems.