Parallel Lines Transversals and Algebra Worksheet Solutions
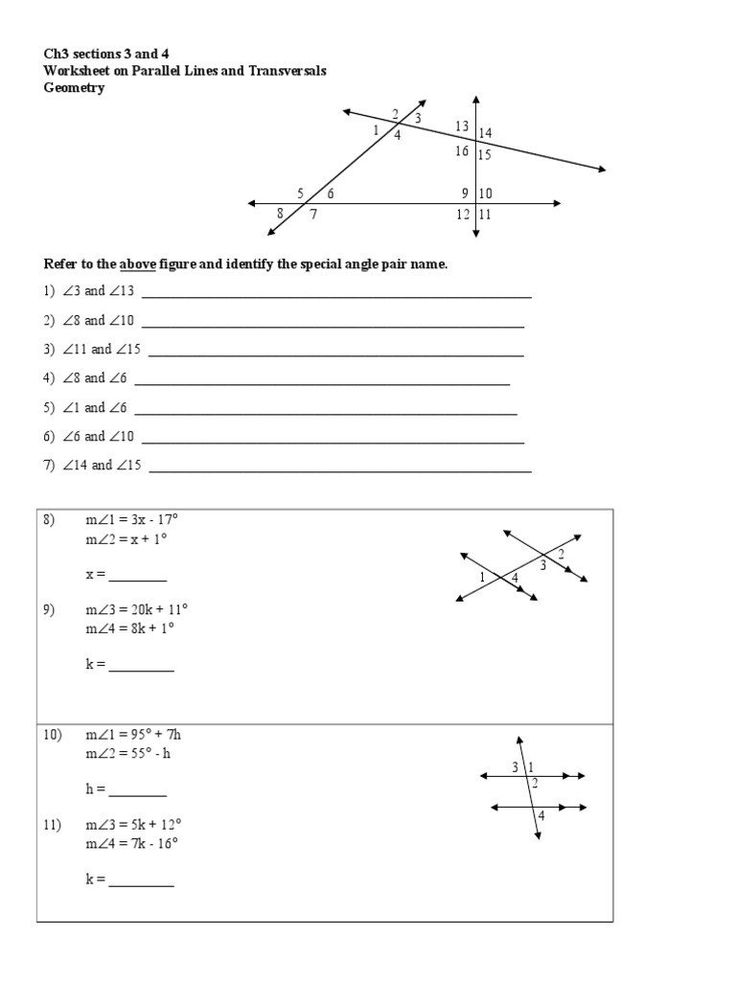
Understanding Parallel Lines, Transversals, and Algebra
In geometry, parallel lines are lines that lie in the same plane and never intersect, no matter how far they are extended. A transversal is a line that intersects two or more lines. When a transversal intersects two parallel lines, it creates pairs of congruent angles. These angles can be used to solve problems involving parallel lines and transversals.
Types of Angles Formed by Parallel Lines and Transversals
When a transversal intersects two parallel lines, it forms several types of angles:
- Corresponding Angles: These are angles that are in the same position on each line.
- Alternate Interior Angles: These are angles that are on opposite sides of the transversal and inside the parallel lines.
- Alternate Exterior Angles: These are angles that are on opposite sides of the transversal and outside the parallel lines.
- Interior Angles on the Same Side of the Transversal: These are angles that are on the same side of the transversal and inside the parallel lines.
- Exterior Angles on the Same Side of the Transversal: These are angles that are on the same side of the transversal and outside the parallel lines.
Properties of Angles Formed by Parallel Lines and Transversals
The angles formed by parallel lines and transversals have the following properties:
- Corresponding Angles are Congruent: If two lines are parallel, then the corresponding angles are congruent.
- Alternate Interior Angles are Congruent: If two lines are parallel, then the alternate interior angles are congruent.
- Alternate Exterior Angles are Congruent: If two lines are parallel, then the alternate exterior angles are congruent.
- Interior Angles on the Same Side of the Transversal are Supplementary: If two lines are parallel, then the interior angles on the same side of the transversal are supplementary.
Using Algebra to Solve Problems Involving Parallel Lines and Transversals
Algebra can be used to solve problems involving parallel lines and transversals by representing the angles as variables and using the properties of angles to set up equations.
For example, if we have two parallel lines intersected by a transversal, and the corresponding angles are 3x and 2x, we can set up the equation:
3x = 2x + 30
To solve for x, we can add 2x to both sides of the equation:
5x = 30
Then, we can divide both sides of the equation by 5:
x = 6
Therefore, the corresponding angles are 3(6) = 18 and 2(6) = 12.
Worksheet Solutions
Here are some worksheet solutions involving parallel lines and transversals:

| Problem | Solution |
|---|---|
| In the diagram, line AB is parallel to line CD. If angle A is 30 degrees, what is the measure of angle C? | Since angle A and angle C are corresponding angles, they are congruent. Therefore, angle C is also 30 degrees. |
| In the diagram, line EF is parallel to line GH. If angle E is 45 degrees, what is the measure of angle G? | Since angle E and angle G are alternate interior angles, they are congruent. Therefore, angle G is also 45 degrees. |
| In the diagram, line JK is parallel to line LM. If angle J is 2x and angle M is 3x, what is the measure of angle J? | Since angle J and angle M are corresponding angles, they are congruent. We can set up the equation: 2x = 3x - 20. Solving for x, we get x = 20. Therefore, angle J is 2(20) = 40 degrees. |
📝 Note: These are just a few examples of how algebra can be used to solve problems involving parallel lines and transversals. There are many more problems and solutions that can be created using these concepts.
In summary, parallel lines and transversals form pairs of congruent angles that can be used to solve problems. Algebra can be used to represent these angles as variables and set up equations to solve for unknown values. By understanding the properties of angles formed by parallel lines and transversals, we can use algebra to solve a wide range of problems.
What is the difference between corresponding angles and alternate interior angles?
+Corresponding angles are angles that are in the same position on each line, while alternate interior angles are angles that are on opposite sides of the transversal and inside the parallel lines.
How can algebra be used to solve problems involving parallel lines and transversals?
+Algebra can be used to represent angles as variables and set up equations to solve for unknown values. By using the properties of angles formed by parallel lines and transversals, we can set up equations to solve for unknown angles.
What is the property of interior angles on the same side of the transversal?
+Interior angles on the same side of the transversal are supplementary, meaning that they add up to 180 degrees.