6 Ways to Master Parallel Lines and Transversals

Mastering parallel lines and transversals is a fundamental concept in geometry that can help you solve various problems and theorems. In this article, we will explore six ways to master parallel lines and transversals, including understanding the basics, identifying corresponding angles, and applying the properties of parallel lines.
Understanding the Basics
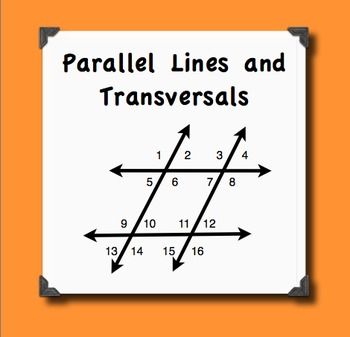
To master parallel lines and transversals, you need to understand the basic concepts. Parallel lines are lines that lie in the same plane and never intersect, no matter how far they are extended. Transversals, on the other hand, are lines that intersect two or more parallel lines.
| Parallel Lines | Transversals |
|---|---|
| Lines that lie in the same plane and never intersect | Lines that intersect two or more parallel lines |
Identifying Corresponding Angles
When a transversal intersects two parallel lines, it forms corresponding angles. Corresponding angles are angles that have the same measure and are located in the same relative position.
- When a transversal intersects two parallel lines, the corresponding angles are equal.
- The corresponding angles are located in the same relative position, such as the upper left or lower right.
📝 Note: Corresponding angles are used to prove that two lines are parallel.
Applying the Properties of Parallel Lines
Parallel lines have several properties that can be used to solve problems and theorems. Some of these properties include:
- Alternate Interior Angles: When a transversal intersects two parallel lines, the alternate interior angles are equal.
- Alternate Exterior Angles: When a transversal intersects two parallel lines, the alternate exterior angles are equal.
- Interior Angles on the Same Side of the Transversal: When a transversal intersects two parallel lines, the interior angles on the same side of the transversal are supplementary.
| Property | Description |
|---|---|
| Alternate Interior Angles | Equal angles that are located on opposite sides of the transversal |
| Alternate Exterior Angles | Equal angles that are located on opposite sides of the transversal |
| Interior Angles on the Same Side of the Transversal | Supplementary angles that are located on the same side of the transversal |
Using the Transversal Theorem
The Transversal Theorem states that if two parallel lines are cut by a transversal, then the corresponding angles are equal. This theorem can be used to prove that two lines are parallel.
- If two lines are cut by a transversal and the corresponding angles are equal, then the lines are parallel.
- If two lines are parallel and a transversal intersects them, then the corresponding angles are equal.
📝 Note: The Transversal Theorem is used to prove that two lines are parallel.
Applying the Converse of the Transversal Theorem
The Converse of the Transversal Theorem states that if two lines are cut by a transversal and the corresponding angles are equal, then the lines are parallel.
- If two lines are cut by a transversal and the corresponding angles are equal, then the lines are parallel.
- If two lines are parallel and a transversal intersects them, then the corresponding angles are equal.
📝 Note: The Converse of the Transversal Theorem is used to prove that two lines are parallel.
Practicing with Examples
Practicing with examples is essential to mastering parallel lines and transversals. Here are a few examples to get you started:
- If two parallel lines are cut by a transversal, what is the relationship between the corresponding angles?
- If two lines are cut by a transversal and the corresponding angles are equal, what can be concluded about the lines?
By practicing with examples and applying the properties of parallel lines, you can master parallel lines and transversals.
In summary, mastering parallel lines and transversals requires understanding the basics, identifying corresponding angles, applying the properties of parallel lines, using the Transversal Theorem, applying the Converse of the Transversal Theorem, and practicing with examples. By following these steps, you can become proficient in solving problems and theorems related to parallel lines and transversals.
What are parallel lines?
+Parallel lines are lines that lie in the same plane and never intersect, no matter how far they are extended.
What is a transversal?
+A transversal is a line that intersects two or more parallel lines.
What is the relationship between corresponding angles?
+Corresponding angles are equal and are located in the same relative position.