5 Tips to Master Parallel Lines and Transversal

Understanding Parallel Lines and Transversal

Parallel lines and transversal are fundamental concepts in geometry that can seem daunting at first, but with practice and patience, you can master them. In this article, we will explore five tips to help you better understand and work with parallel lines and transversal.

Tip 1: Define Parallel Lines and Transversal

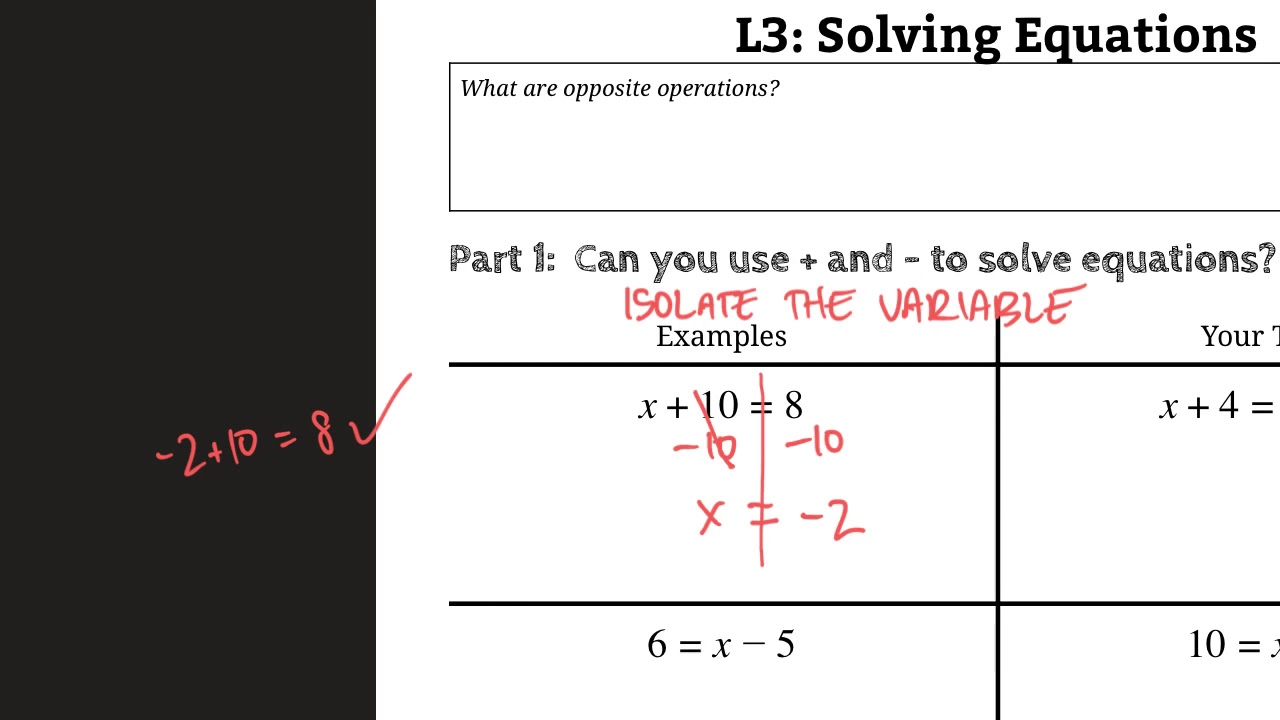
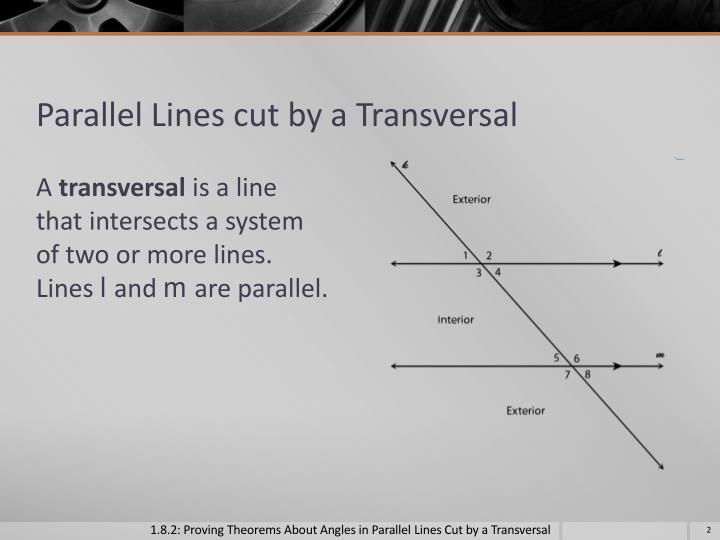
Before diving into the tips, let’s define parallel lines and transversal. Parallel lines are two or more lines that lie in the same plane and never intersect, no matter how far they are extended. A transversal, on the other hand, is a line that intersects two or more lines. When a transversal intersects two parallel lines, it forms pairs of congruent angles.

Tip 2: Identify Types of Angles Formed by Parallel Lines and Transversal

When a transversal intersects two parallel lines, it forms several types of angles, including:

• Corresponding angles: These are angles that are in the same relative position in each intersection.
• Alternate interior angles: These are angles that are on opposite sides of the transversal and inside the parallel lines.
• Alternate exterior angles: These are angles that are on opposite sides of the transversal and outside the parallel lines.
• Interior angles on the same side of the transversal: These are angles that are on the same side of the transversal and inside the parallel lines.

Understanding these types of angles is crucial in working with parallel lines and transversal.

Tip 3: Use Properties of Parallel Lines and Transversal to Solve Problems

Here are some properties of parallel lines and transversal that you can use to solve problems:

• Corresponding angles are congruent: If two lines are parallel, then the corresponding angles formed by a transversal are congruent.
• Alternate interior angles are congruent: If two lines are parallel, then the alternate interior angles formed by a transversal are congruent.
• Alternate exterior angles are congruent: If two lines are parallel, then the alternate exterior angles formed by a transversal are congruent.
• Interior angles on the same side of the transversal are supplementary: If two lines are parallel, then the interior angles on the same side of the transversal are supplementary.

These properties can help you solve problems involving parallel lines and transversal.

Tip 4: Practice, Practice, Practice

Practice is key to mastering parallel lines and transversal. Here are some tips to help you practice:

• Draw diagrams: Draw diagrams of parallel lines and transversal to visualize the concepts.
• Work on sample problems: Work on sample problems to practice applying the properties of parallel lines and transversal.
• Use online resources: Use online resources, such as interactive geometry software, to practice and explore parallel lines and transversal.

The more you practice, the more comfortable you will become with parallel lines and transversal.

Tip 5: Apply Parallel Lines and Transversal to Real-World Problems

Parallel lines and transversal have many real-world applications, such as:

• Architecture: Architects use parallel lines and transversal to design buildings and bridges.
• Engineering: Engineers use parallel lines and transversal to design roads and highways.
• Art: Artists use parallel lines and transversal to create perspective and depth in their artwork.

By applying parallel lines and transversal to real-world problems, you can see the relevance and importance of these concepts.

📝 Note: Remember to always check your work and verify your answers when working with parallel lines and transversal.

In summary, mastering parallel lines and transversal requires understanding the definitions and properties of these concepts, practicing problems, and applying them to real-world problems. By following these tips, you can become proficient in working with parallel lines and transversal.