5 Ways to Master Parallel Circuits Worksheet

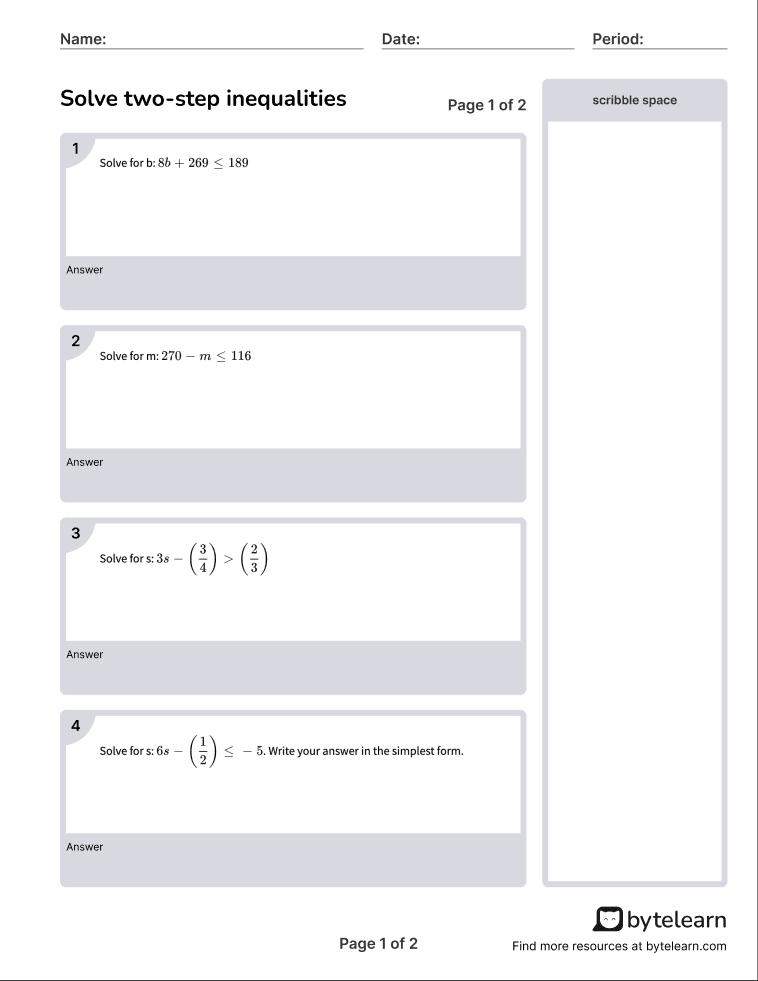
Understanding the Basics of Parallel Circuits
Parallel circuits are an essential part of electrical engineering and electronics. Unlike series circuits, where components are connected one after the other, parallel circuits have components connected between the same two points, allowing the current to flow through each component independently. Mastering parallel circuits is crucial for designing and analyzing complex electrical systems. In this post, we will explore five ways to master parallel circuits using worksheets.
Method 1: Calculate Total Resistance in Parallel Circuits
Calculating total resistance in parallel circuits is a fundamental concept. The formula for calculating total resistance in parallel circuits is:
1/Rt = 1/R1 + 1/R2 + 1/R3 +…
Where Rt is the total resistance, and R1, R2, R3 are the individual resistances.
Example Problem:
Three resistors with resistances of 2Ω, 4Ω, and 6Ω are connected in parallel. Calculate the total resistance.
Solution:
1/Rt = 1⁄2 + 1⁄4 + 1⁄6 1/Rt = 0.5 + 0.25 + 0.17 1/Rt = 0.92 Rt = 1.09Ω
Practice Exercise:
Calculate the total resistance in the following parallel circuit:
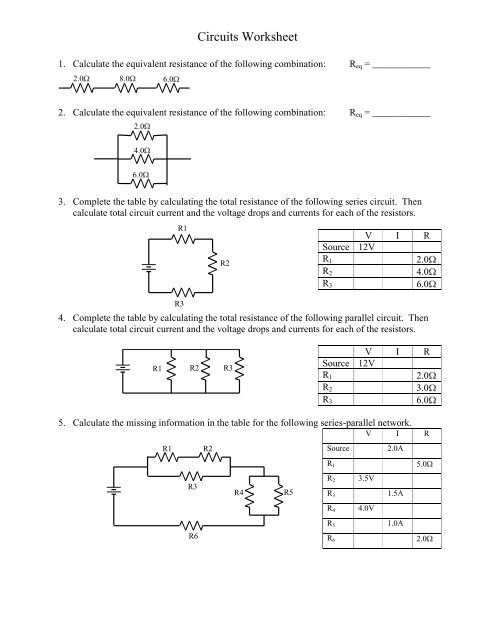
| Resistor | Resistance (Ω) |
|---|---|
| R1 | 3 |
| R2 | 6 |
| R3 | 9 |
Method 2: Calculate Voltage and Current in Parallel Circuits
In parallel circuits, the voltage across each component is the same, while the current through each component may vary.
Example Problem:
A 12V battery is connected to a parallel circuit with three resistors of 2Ω, 4Ω, and 6Ω. Calculate the voltage and current through each resistor.
Solution:
The voltage across each resistor is the same, which is 12V.
The current through each resistor can be calculated using Ohm’s law:
I = V/R
I1 = 12⁄2 = 6A I2 = 12⁄4 = 3A I3 = 12⁄6 = 2A
Practice Exercise:
Calculate the voltage and current through each resistor in the following parallel circuit:
| Resistor | Resistance (Ω) |
|---|---|
| R1 | 3 |
| R2 | 6 |
| R3 | 9 |
Voltage: _______________________
Current:
- I1: _______________________
- I2: _______________________
- I3: _______________________
Method 3: Analyze Parallel Circuits with Multiple Voltage Sources
In some cases, parallel circuits may have multiple voltage sources. To analyze such circuits, we need to calculate the total voltage and current.
Example Problem:
A parallel circuit has two voltage sources of 12V and 6V, connected to three resistors of 2Ω, 4Ω, and 6Ω. Calculate the total voltage and current.
Solution:
To calculate the total voltage, we need to calculate the equivalent voltage source:
Veq = V1 + V2 Veq = 12 + 6 Veq = 18V
The total current can be calculated using Ohm’s law:
I = Veq/Rt
First, we need to calculate the total resistance:
1/Rt = 1⁄2 + 1⁄4 + 1⁄6 1/Rt = 0.5 + 0.25 + 0.17 1/Rt = 0.92 Rt = 1.09Ω
I = 18⁄1.09 I = 16.51A
Practice Exercise:
Analyze the following parallel circuit with multiple voltage sources:
| Voltage Source | Voltage (V) |
|---|---|
| V1 | 9 |
| V2 | 3 |
| Resistor | Resistance (Ω) |
|---|---|
| R1 | 3 |
| R2 | 6 |
| R3 | 9 |
Calculate the total voltage and current:
Total Voltage: _______________________ Total Current: _______________________
Method 4: Use Kirchhoff's Current Law (KCL) to Analyze Parallel Circuits
Kirchhoff’s Current Law (KCL) states that the total current entering a node is equal to the total current leaving the node.
Example Problem:
A parallel circuit has three resistors of 2Ω, 4Ω, and 6Ω, connected to a voltage source of 12V. Use KCL to calculate the current through each resistor.
Solution:
The current through each resistor can be calculated using KCL:
I1 + I2 + I3 = I
where I is the total current.
Using Ohm’s law, we can calculate the current through each resistor:
I1 = 12⁄2 = 6A I2 = 12⁄4 = 3A I3 = 12⁄6 = 2A
I = I1 + I2 + I3 I = 6 + 3 + 2 I = 11A
Practice Exercise:
Use KCL to analyze the following parallel circuit:
| Resistor | Resistance (Ω) |
|---|---|
| R1 | 3 |
| R2 | 6 |
| R3 | 9 |
Voltage: 12V
Calculate the current through each resistor:
I1: _______________________ I2: _______________________ I3: _______________________
Method 5: Use Kirchhoff's Voltage Law (KVL) to Analyze Parallel Circuits
Kirchhoff’s Voltage Law (KVL) states that the total voltage around a closed loop is zero.
Example Problem:
A parallel circuit has three resistors of 2Ω, 4Ω, and 6Ω, connected to a voltage source of 12V. Use KVL to calculate the voltage across each resistor.
Solution:
The voltage across each resistor can be calculated using KVL:
V1 + V2 + V3 = V
where V is the total voltage.
Using Ohm’s law, we can calculate the voltage across each resistor:
V1 = I1 x R1 V2 = I2 x R2 V3 = I3 x R3
V = V1 + V2 + V3 V = 12
Practice Exercise:
Use KVL to analyze the following parallel circuit:
| Resistor | Resistance (Ω) |
|---|---|
| R1 | 3 |
| R2 | 6 |
| R3 | 9 |
Voltage: 12V
Calculate the voltage across each resistor:
V1: _______________________ V2: _______________________ V3: _______________________
💡 Note: To master parallel circuits, it's essential to practice solving problems using different methods and techniques.
To recap, we’ve explored five ways to master parallel circuits using worksheets. By practicing these methods, you’ll become proficient in analyzing and designing complex electrical systems.
What is the main difference between series and parallel circuits?
+
In series circuits, components are connected one after the other, while in parallel circuits, components are connected between the same two points, allowing the current to flow through each component independently.
How do you calculate total resistance in parallel circuits?
+
The formula for calculating total resistance in parallel circuits is: 1/Rt = 1/R1 + 1/R2 + 1/R3 +…
What is Kirchhoff’s Current Law (KCL)?
+
Kirchhoff’s Current Law (KCL) states that the total current entering a node is equal to the total current leaving the node.
Related Terms:
- Parallel Circuits Worksheet pdf