Parallel and Perpendicular Lines Practice Worksheet
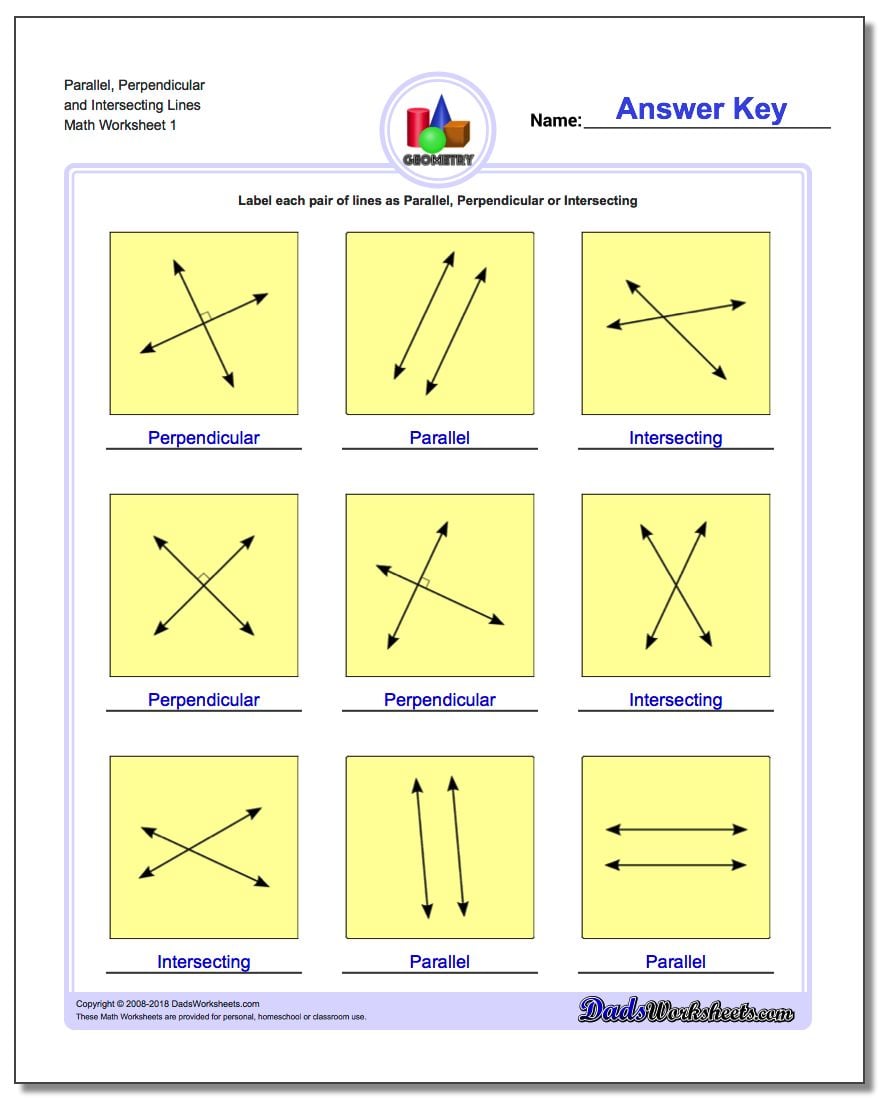
Parallel and Perpendicular Lines: A Comprehensive Guide
Lines are a fundamental concept in geometry, and understanding their properties is crucial for solving various problems. Two essential types of lines are parallel and perpendicular lines. In this article, we will delve into the world of parallel and perpendicular lines, exploring their definitions, properties, and real-world applications.
What are Parallel Lines?
Parallel lines are lines that lie in the same plane and never intersect, no matter how far they are extended. In other words, they have the same slope and are always at the same distance from each other. Parallel lines can be represented by the following equation:
y = mx + b
where m is the slope and b is the y-intercept.
Key Properties of Parallel Lines:
- They never intersect.
- They have the same slope (m).
- They are always at the same distance from each other.
What are Perpendicular Lines?
Perpendicular lines, on the other hand, are lines that intersect at a 90-degree angle (a right angle). When two lines intersect perpendicularly, they form a right angle, and the product of their slopes is -1.
Key Properties of Perpendicular Lines:
- They intersect at a 90-degree angle.
- The product of their slopes is -1.
- They are not parallel.
Identifying Parallel and Perpendicular Lines
To determine if two lines are parallel or perpendicular, you can use the following methods:
- Slope Method: Compare the slopes of the two lines. If the slopes are equal, the lines are parallel. If the product of the slopes is -1, the lines are perpendicular.
- Graphing Method: Plot the two lines on a graph. If the lines never intersect, they are parallel. If the lines intersect at a 90-degree angle, they are perpendicular.
Real-World Applications of Parallel and Perpendicular Lines
Parallel and perpendicular lines have numerous real-world applications in:
- Architecture: Builders use parallel and perpendicular lines to design and construct buildings, ensuring stability and structural integrity.
- Engineering: Engineers rely on parallel and perpendicular lines to design and build complex systems, such as bridges and roller coasters.
- Art and Design: Artists and designers use parallel and perpendicular lines to create visually appealing compositions and designs.
Practice Problems
Here are some practice problems to help you reinforce your understanding of parallel and perpendicular lines:
Parallel Lines:
- Are the lines represented by the equations y = 2x + 1 and y = 2x + 3 parallel? Why or why not?
- Write an equation for a line that is parallel to the line y = 3x - 2.
Perpendicular Lines:
- Are the lines represented by the equations y = 4x - 1 and y = -1/4x + 2 perpendicular? Why or why not?
- Write an equation for a line that is perpendicular to the line y = 2x + 1.
📝 Note: For more practice problems, visit our website or consult your textbook.
Conclusion
In conclusion, understanding parallel and perpendicular lines is essential for problem-solving in geometry and various real-world applications. By recognizing the properties and characteristics of these lines, you can tackle complex problems with confidence. Remember to practice regularly to reinforce your understanding and become proficient in identifying and working with parallel and perpendicular lines.
What is the difference between parallel and perpendicular lines?
+Parallel lines are lines that lie in the same plane and never intersect, while perpendicular lines intersect at a 90-degree angle.
How do I determine if two lines are parallel or perpendicular?
+You can use the slope method or graphing method to determine if two lines are parallel or perpendicular.
What are some real-world applications of parallel and perpendicular lines?
+Parallel and perpendicular lines have applications in architecture, engineering, art, and design.