Order of Operations With Fractions Made Easy

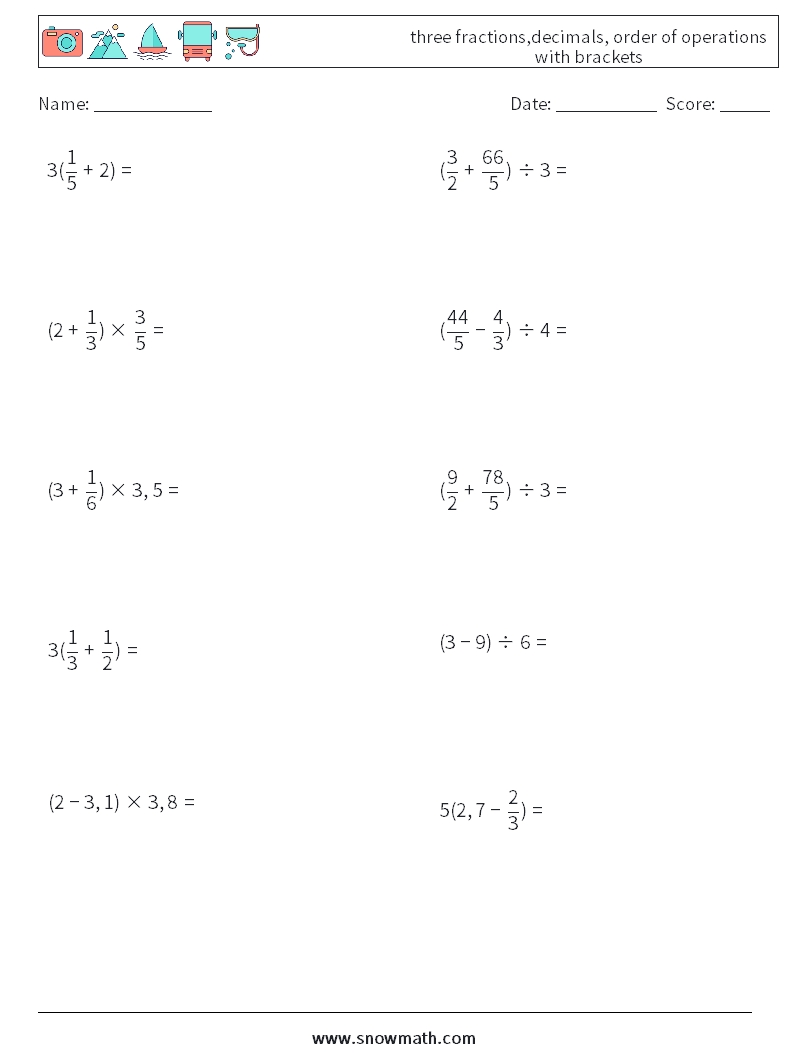
Unlocking the Secrets of Order of Operations with Fractions

When it comes to solving mathematical expressions involving fractions, the order of operations can be a daunting task. However, with the right approach, you can master this skill and become a pro at simplifying complex expressions. In this article, we’ll explore the world of order of operations with fractions and provide you with a step-by-step guide to make it easy.

What is the Order of Operations?

The order of operations is a set of rules that dictates the order in which mathematical operations should be performed when there are multiple operations in an expression. The acronym PEMDAS is commonly used to remember the order of operations:

• Parentheses: Evaluate expressions inside parentheses first.
• Exponents: Evaluate any exponential expressions next (e.g., 2^3).
• Multiplication and Division: Evaluate multiplication and division operations from left to right.
• Addition and Subtraction: Finally, evaluate any addition and subtraction operations from left to right.

How to Apply the Order of Operations with Fractions

When working with fractions, it’s essential to apply the order of operations carefully to avoid errors. Here’s a step-by-step guide to help you simplify expressions with fractions:

1. Evaluate expressions inside parentheses: If there are any expressions inside parentheses, evaluate them first.
2. Simplify any exponential expressions: If there are any exponential expressions, simplify them next.
3. Simplify any multiplication and division operations: Evaluate any multiplication and division operations from left to right. When multiplying or dividing fractions, follow these rules:
   • Multiply the numerators (the numbers on top) and multiply the denominators (the numbers on the bottom).
   • Divide the numerator of the first fraction by the denominator of the second fraction.
4. Simplify any addition and subtraction operations: Finally, evaluate any addition and subtraction operations from left to right. When adding or subtracting fractions, follow these rules:
   • Find a common denominator (the least common multiple of the two denominators).
   • Convert each fraction to have the common denominator.
   • Add or subtract the numerators.

📝 Note: When working with fractions, it's essential to simplify each step carefully to avoid errors.

Example Problems

Let’s practice applying the order of operations with fractions using some example problems.

Problem 1

Simplify the expression: 2 × (³⁄₄) + ¹⁄₂

Solution

1. Evaluate the expression inside the parentheses: ³⁄₄.
2. Multiply 2 by ³⁄₄: 2 × ³⁄₄ = ⁶⁄₄.
3. Simplify the result: ⁶⁄₄ = ³⁄₂.
4. Add ¹⁄₂ to the result: ³⁄₂ + ¹⁄₂ = ⁴⁄₂.
5. Simplify the final result: ⁴⁄₂ = 2.

Problem 2

Simplify the expression: ¹⁄₂ + ³⁄₄ - ²⁄₃

Solution

1. Find a common denominator: 12.
2. Convert each fraction to have the common denominator:
   • ¹⁄₂ = ⁶⁄₁₂.
   • ³⁄₄ = ⁹⁄₁₂.
   • ²⁄₃ = ⁸⁄₁₂.
3. Add and subtract the fractions: ⁶⁄₁₂ + ⁹⁄₁₂ - ⁸⁄₁₂ = ⁷⁄₁₂.

Conclusion

Mastering the order of operations with fractions takes practice, but with this step-by-step guide, you’ll be well on your way to becoming a pro at simplifying complex expressions. Remember to always follow the order of operations carefully and simplify each step to avoid errors. With time and practice, you’ll become more confident and proficient in your ability to work with fractions.