5 Ways to Master Multiplying Exponents
Understanding Exponents and Their Importance
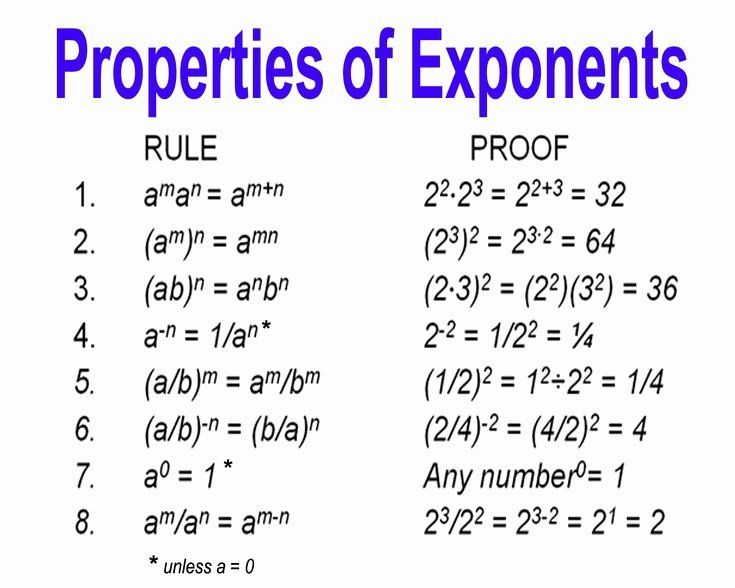
Exponents are a fundamental concept in mathematics, and mastering them is crucial for success in various mathematical disciplines, including algebra, geometry, and calculus. Exponents are used to represent repeated multiplication of a number by itself, and they play a critical role in simplifying complex mathematical expressions. In this article, we will focus on multiplying exponents, a skill that requires a deep understanding of exponent rules and properties.
Rule 1: Multiplying Exponents with the Same Base
When multiplying exponents with the same base, the rule is to add the exponents. This rule applies to both positive and negative exponents. For example:
2^3 × 2^4 = 2^(3+4) = 2^7
In this example, the base is 2, and the exponents are 3 and 4. By adding the exponents, we get 2^7.
📝 Note: When multiplying exponents with the same base, make sure to add the exponents, not the bases.
Rule 2: Multiplying Exponents with Different Bases
When multiplying exponents with different bases, the rule is to multiply the bases and add the exponents. However, this rule only applies when the bases are the same. If the bases are different, the expression cannot be simplified further. For example:
2^3 × 3^4 = (2 × 3)^(3+4) = 6^7
However, if the bases are different, the expression remains the same:
2^3 × 3^4 = 2^3 × 3^4
📝 Note: When multiplying exponents with different bases, the expression cannot be simplified further unless the bases are the same.
Rule 3: Multiplying Exponents with Negative Exponents
When multiplying exponents with negative exponents, the rule is to add the exponents. However, when dealing with negative exponents, it’s essential to remember that a negative exponent represents a reciprocal. For example:
2^(-3) × 2^4 = 2^(-3+4) = 2^1
In this example, the negative exponent -3 represents a reciprocal, and adding 4 results in 2^1.
📝 Note: When dealing with negative exponents, remember that they represent reciprocals.
Rule 4: Multiplying Exponents with Fractional Exponents
When multiplying exponents with fractional exponents, the rule is to add the exponents. However, when dealing with fractional exponents, it’s essential to remember that they represent roots. For example:
2^(1⁄2) × 2^(1⁄3) = 2^(1⁄2+1⁄3) = 2^(5⁄6)
In this example, the fractional exponents represent roots, and adding them results in 2^(5⁄6).
📝 Note: When dealing with fractional exponents, remember that they represent roots.
Rule 5: Simplifying Expressions with Multiple Exponents
When simplifying expressions with multiple exponents, it’s essential to apply the rules mentioned above. For example:
2^3 × 2^(-2) × 3^4 = 2^(3-2) × 3^4 = 2^1 × 3^4
In this example, we applied the rules mentioned above to simplify the expression.
📝 Note: When simplifying expressions with multiple exponents, apply the rules mentioned above to simplify the expression.
What is the rule for multiplying exponents with the same base?
+When multiplying exponents with the same base, the rule is to add the exponents.
Can I simplify expressions with different bases?
+No, expressions with different bases cannot be simplified further unless the bases are the same.
How do I deal with negative exponents?
+Negative exponents represent reciprocals, so when multiplying exponents with negative exponents, add the exponents.
Mastering multiplying exponents requires a deep understanding of exponent rules and properties. By applying the rules mentioned above, you can simplify complex mathematical expressions and improve your math skills. Remember to add exponents when multiplying exponents with the same base, and be cautious when dealing with negative and fractional exponents. With practice and patience, you can become proficient in multiplying exponents and tackle even the most challenging math problems.