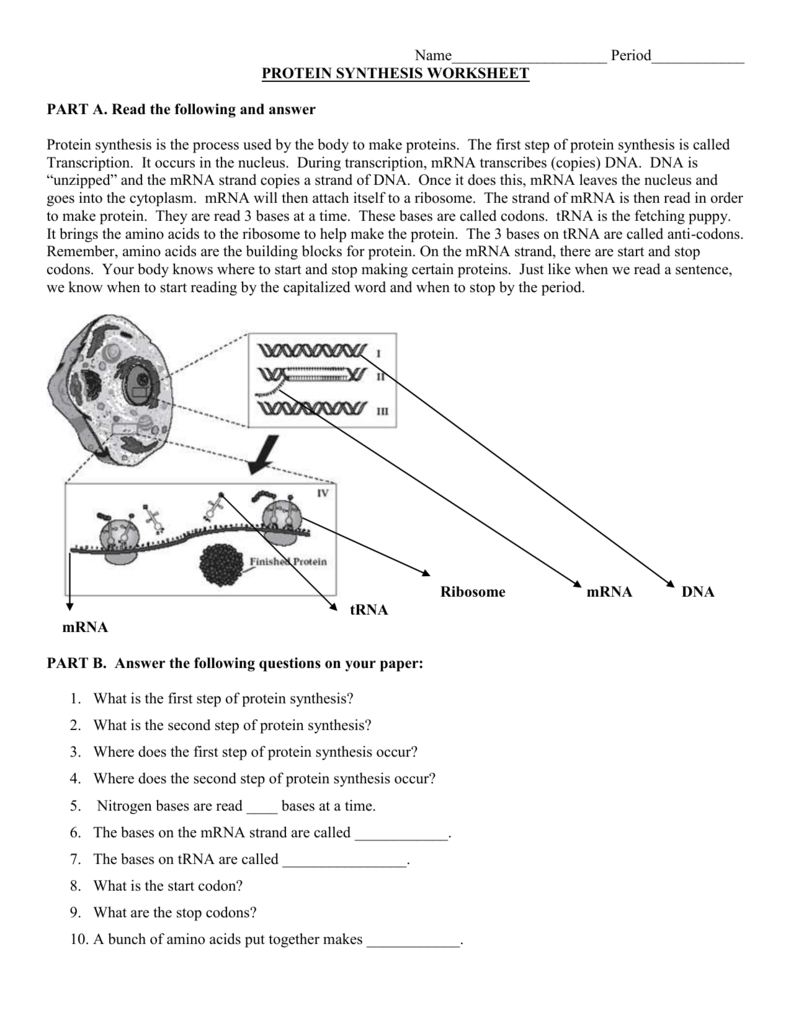
5 Key Multiplication Properties to Master

Understanding Multiplication Properties
Multiplication is one of the fundamental operations in mathematics, and mastering its properties is essential for solving various mathematical problems. In this blog post, we will explore five key multiplication properties that you should know.
The Commutative Property of Multiplication
The commutative property of multiplication states that the order of the factors does not change the product. In other words, a × b = b × a. This property allows us to rearrange the factors in a multiplication problem without changing the result.
For example:
- 2 × 3 = 3 × 2 = 6
- 4 × 5 = 5 × 4 = 20
📝 Note: The commutative property also applies to addition, but not to subtraction or division.
The Associative Property of Multiplication
The associative property of multiplication states that when we multiply three or more numbers, the grouping of the numbers does not affect the product. In other words, (a × b) × c = a × (b × c). This property allows us to regroup the numbers in a multiplication problem without changing the result.
For example:
- (2 × 3) × 4 = 2 × (3 × 4) = 24
- (5 × 2) × 3 = 5 × (2 × 3) = 30
📝 Note: The associative property also applies to addition, but not to subtraction or division.
The Distributive Property of Multiplication over Addition
The distributive property of multiplication over addition states that when we multiply a number by the sum of two or more numbers, we can distribute the multiplication to each addend. In other words, a × (b + c) = a × b + a × c. This property allows us to simplify multiplication problems by distributing the multiplication to each addend.
For example:
- 2 × (3 + 4) = 2 × 3 + 2 × 4 = 14
- 5 × (2 + 6) = 5 × 2 + 5 × 6 = 40
The Multiplication Property of Zero
The multiplication property of zero states that when we multiply any number by zero, the result is always zero. In other words, a × 0 = 0. This property may seem obvious, but it is essential to understand that any number multiplied by zero results in zero.
For example:
- 2 × 0 = 0
- 5 × 0 = 0
The Multiplication Property of One
The multiplication property of one states that when we multiply any number by one, the result is always the same number. In other words, a × 1 = a. This property may seem obvious, but it is essential to understand that any number multiplied by one results in the same number.
For example:
- 2 × 1 = 2
- 5 × 1 = 5

| Property | Statement | Example |
|---|---|---|
| Commutative Property | a × b = b × a | 2 × 3 = 3 × 2 = 6 |
| Associative Property | (a × b) × c = a × (b × c) | (2 × 3) × 4 = 2 × (3 × 4) = 24 |
| Distributive Property | a × (b + c) = a × b + a × c | 2 × (3 + 4) = 2 × 3 + 2 × 4 = 14 |
| Multiplication Property of Zero | a × 0 = 0 | 2 × 0 = 0 |
| Multiplication Property of One | a × 1 = a | 2 × 1 = 2 |
Mastering these five key multiplication properties will help you solve various mathematical problems with ease. Remember to apply these properties to simplify multiplication problems and make calculations more efficient.
In conclusion, understanding the commutative, associative, distributive, and multiplication properties of zero and one is crucial for mastering multiplication. By applying these properties, you can simplify complex multiplication problems and become more proficient in mathematics.
What is the commutative property of multiplication?
+The commutative property of multiplication states that the order of the factors does not change the product. In other words, a × b = b × a.
What is the distributive property of multiplication over addition?
+The distributive property of multiplication over addition states that when we multiply a number by the sum of two or more numbers, we can distribute the multiplication to each addend. In other words, a × (b + c) = a × b + a × c.
What is the multiplication property of zero?
+The multiplication property of zero states that when we multiply any number by zero, the result is always zero. In other words, a × 0 = 0.
Related Terms:
- Properties of multiplication Worksheet PDF