Solving Multiple Step Equations Made Easy
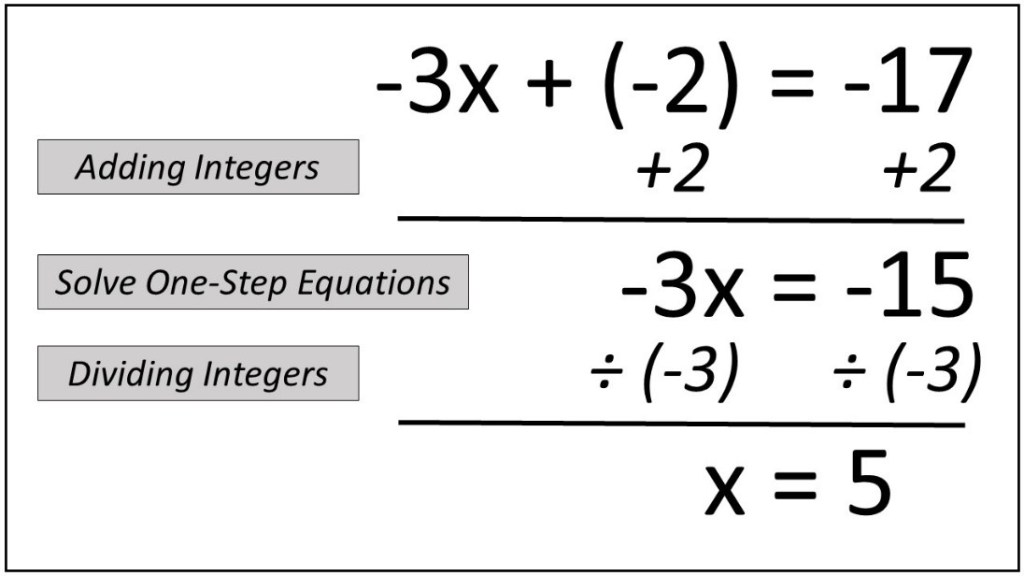
Breaking Down the Problem: Understanding Multiple Step Equations
When it comes to solving equations, many students find themselves struggling with the complexity of multiple step equations. These types of equations require a combination of mathematical operations to isolate the variable, which can be overwhelming if not approached in a systematic way. In this article, we will break down the problem of solving multiple step equations into manageable steps, providing you with a clear understanding of how to tackle these equations with confidence.
The Basics: Understanding the Structure of Multiple Step Equations
Multiple step equations are linear equations that require more than one step to solve. They typically involve a combination of addition, subtraction, multiplication, and division operations, as well as the presence of constants and coefficients. The general structure of a multiple step equation can be represented as:
ax + b = c
where ‘a’ is the coefficient of the variable ‘x’, ‘b’ is the constant term, and ‘c’ is the constant term on the right-hand side of the equation.
Step-by-Step Guide to Solving Multiple Step Equations
Solving multiple step equations requires a logical and systematic approach. Here’s a step-by-step guide to help you solve these equations:
Step 1: Simplify the Equation
Begin by simplifying the equation by combining like terms. This involves adding or subtracting constants and coefficients to isolate the variable.
Step 2: Eliminate the Constant Term
Next, eliminate the constant term on the same side as the variable by adding or subtracting the same value to both sides of the equation.
Step 3: Isolate the Variable
Now, isolate the variable by performing the necessary operations to get the variable alone on one side of the equation.
Step 4: Check Your Solution
Finally, check your solution by plugging the value back into the original equation to ensure it is true.
🤔 Note: Always check your solution to ensure accuracy and avoid mistakes.
Example Problems: Putting the Steps into Practice
Let’s work through some example problems to illustrate the steps involved in solving multiple step equations.
Example 1:
Solve for x: 2x + 5 = 11
Step 1: Simplify the Equation
Combine like terms: 2x + 5 = 11
Step 2: Eliminate the Constant Term
Subtract 5 from both sides: 2x = 11 - 5 2x = 6
Step 3: Isolate the Variable
Divide both sides by 2: x = 6 ÷ 2 x = 3
Step 4: Check Your Solution
Plug x = 3 back into the original equation: 2(3) + 5 = 11 6 + 5 = 11 11 = 11
👍 Note: The solution checks out, so x = 3 is the correct solution.
Using Inverse Operations to Solve Multiple Step Equations
Another approach to solving multiple step equations involves using inverse operations. Inverse operations are operations that “undo” each other, such as addition and subtraction, or multiplication and division.
Example 2:
Solve for x: x - 3 = 7
Step 1: Identify the Inverse Operation
Identify the inverse operation of subtraction, which is addition.
Step 2: Apply the Inverse Operation
Add 3 to both sides of the equation: x - 3 + 3 = 7 + 3 x = 10
Step 3: Check Your Solution
Plug x = 10 back into the original equation: 10 - 3 = 7 7 = 7
👍 Note: The solution checks out, so x = 10 is the correct solution.
Common Mistakes to Avoid When Solving Multiple Step Equations
When solving multiple step equations, it’s essential to avoid common mistakes that can lead to incorrect solutions. Here are some common mistakes to watch out for:
- Forgetting to check your solution: Always plug your solution back into the original equation to ensure it is true.
- Mixing up inverse operations: Make sure to apply the correct inverse operation to avoid errors.
- Not combining like terms: Combine like terms to simplify the equation before solving.
Conclusion
Solving multiple step equations requires a logical and systematic approach. By breaking down the problem into manageable steps and using inverse operations, you can solve these equations with confidence. Remember to always check your solution and avoid common mistakes to ensure accuracy. With practice and patience, you’ll become proficient in solving multiple step equations and be well on your way to mastering algebra.
What is the general structure of a multiple step equation?
+The general structure of a multiple step equation is ax + b = c, where ‘a’ is the coefficient of the variable ‘x’, ‘b’ is the constant term, and ‘c’ is the constant term on the right-hand side of the equation.
What is the first step in solving a multiple step equation?
+The first step in solving a multiple step equation is to simplify the equation by combining like terms.
What is the importance of checking your solution in multiple step equations?
+Checking your solution ensures that the solution is accurate and true. It helps to avoid mistakes and ensures that the solution satisfies the original equation.