Mastering Calculus: Mean Value Theorem Made Easy
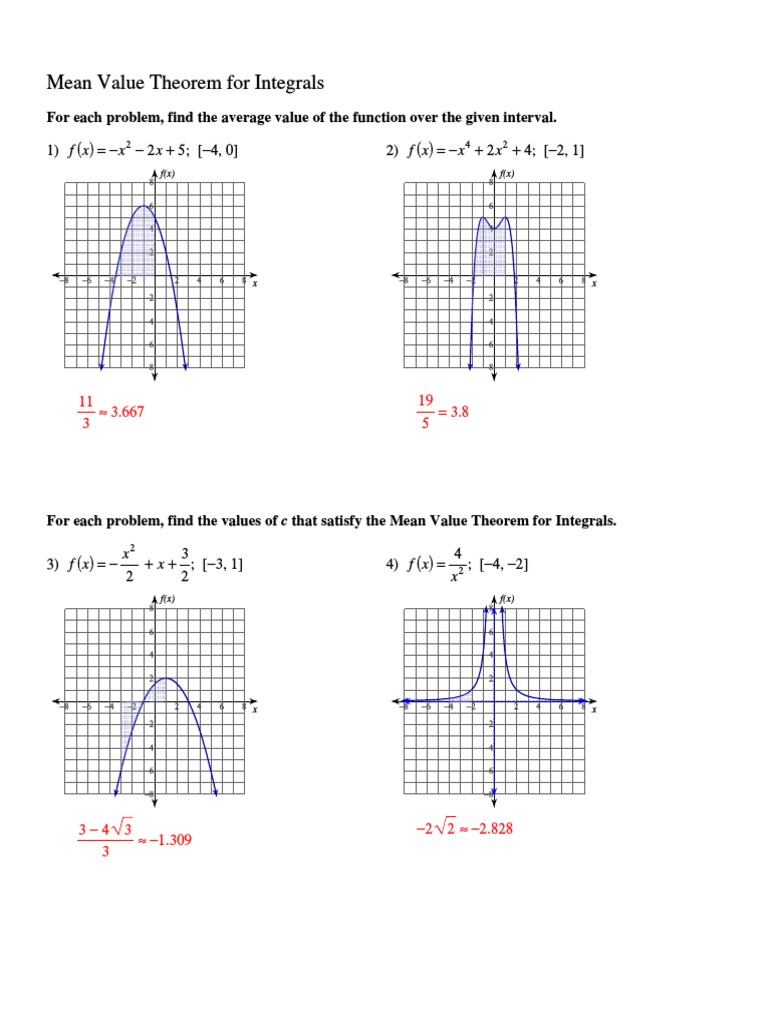
Understanding the Mean Value Theorem (MVT)
The Mean Value Theorem is a fundamental concept in calculus that helps us understand the behavior of functions. It’s a powerful tool for analyzing functions and has numerous applications in physics, engineering, and other fields. In this article, we’ll delve into the world of the Mean Value Theorem, explore its statement, proof, and examples, and provide tips on how to apply it effectively.
What is the Mean Value Theorem?
The Mean Value Theorem states that if a function f(x) is continuous on the closed interval [a, b] and differentiable on the open interval (a, b), then there exists a point c in (a, b) such that the derivative of f at c is equal to the average rate of change of f over [a, b]. Mathematically, this can be expressed as:
f’© = (f(b) - f(a)) / (b - a)
Proof of the Mean Value Theorem
The proof of the Mean Value Theorem involves constructing a new function g(x) that represents the difference between f(x) and the line passing through points (a, f(a)) and (b, f(b)). By applying Rolle’s Theorem to g(x), we can show that there exists a point c in (a, b) where g’© = 0, which leads to the conclusion that f’© = (f(b) - f(a)) / (b - a).
Examples and Applications
The Mean Value Theorem has numerous applications in physics, engineering, and economics. Here are a few examples:
- Motion Along a Line: If an object moves along a line with a constant acceleration, the Mean Value Theorem can be used to determine its instantaneous velocity at any point.
- Economics: The Mean Value Theorem can be used to analyze the behavior of economic systems, such as determining the maximum or minimum of a function.
- Physics: The Mean Value Theorem is used to describe the motion of objects, such as the distance traveled by an object under constant acceleration.
How to Apply the Mean Value Theorem
To apply the Mean Value Theorem effectively, follow these steps:
- Check the conditions: Ensure that the function is continuous on the closed interval [a, b] and differentiable on the open interval (a, b).
- Identify the function: Identify the function f(x) and the interval [a, b].
- Calculate the average rate of change: Calculate the average rate of change of f over [a, b] using the formula (f(b) - f(a)) / (b - a).
- Find the point c: Use the Mean Value Theorem to find the point c in (a, b) where f’© = (f(b) - f(a)) / (b - a).
📝 Note: The Mean Value Theorem is a powerful tool, but it's essential to remember that it only guarantees the existence of a point c, not its uniqueness.
Common Mistakes to Avoid
When applying the Mean Value Theorem, avoid the following common mistakes:
- Ignoring the conditions: Failing to check the conditions of continuity and differentiability can lead to incorrect conclusions.
- Misapplying the theorem: Using the Mean Value Theorem in situations where it’s not applicable can lead to errors.
Conclusion
The Mean Value Theorem is a fundamental concept in calculus that provides valuable insights into the behavior of functions. By understanding its statement, proof, and applications, you can effectively apply it to solve problems and analyze functions. Remember to check the conditions, identify the function, calculate the average rate of change, and find the point c. With practice and patience, you’ll become proficient in using the Mean Value Theorem to tackle complex problems.
What is the main purpose of the Mean Value Theorem?
+
The main purpose of the Mean Value Theorem is to relate the average rate of change of a function over an interval to the instantaneous rate of change at a point within that interval.
What are the conditions for applying the Mean Value Theorem?
+
The conditions for applying the Mean Value Theorem are that the function must be continuous on the closed interval [a, b] and differentiable on the open interval (a, b).
Can the Mean Value Theorem be applied to non-continuous functions?
+
No, the Mean Value Theorem cannot be applied to non-continuous functions. The function must be continuous on the closed interval [a, b] to guarantee the existence of a point c.
Related Terms:
- Average value Theorem practice problems
- Absolute Extrema Worksheet