5 Ways to Master Mean Mode Median Range

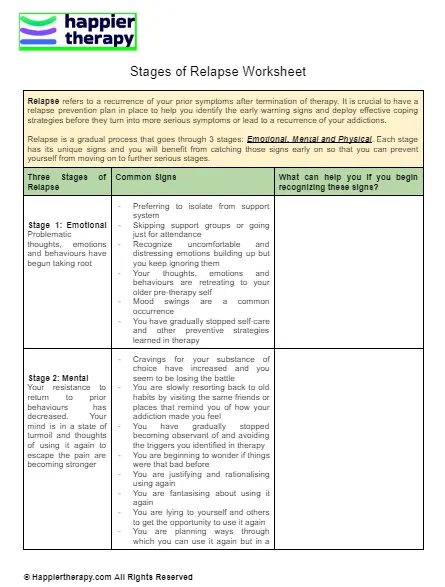
Understanding the Basics of Mean, Mode, Median, and Range
Statistics is a crucial branch of mathematics that deals with the collection, analysis, interpretation, presentation, and organization of data. When it comes to summarizing and describing a dataset, measures of central tendency and variability are essential. In this article, we will delve into the concepts of mean, mode, median, and range, providing you with a comprehensive understanding of these fundamental statistical concepts.
What are Measures of Central Tendency?
Measures of central tendency are statistical tools used to describe the middle or typical value of a dataset. They help us understand the central position of the data and provide a summary of the entire dataset. The three main measures of central tendency are mean, mode, and median.
1. Mean
The mean, also known as the arithmetic mean, is the most commonly used measure of central tendency. It is calculated by summing up all the values in the dataset and dividing by the total number of values. The mean is sensitive to extreme values or outliers in the dataset.
Formula for Mean:
Mean = (Sum of all values) / (Total number of values)
2. Mode
The mode is the most frequently occurring value in the dataset. A dataset may have multiple modes if there are multiple values that appear with the same highest frequency.
Example of Mode:
Suppose we have a dataset of exam scores: 80, 70, 90, 70, 80, 70. The mode is 70, as it appears most frequently.
3. Median
The median is the middle value of the dataset when it is arranged in ascending or descending order. If the dataset has an even number of values, the median is the average of the two middle values.
Example of Median:
Suppose we have a dataset of exam scores: 80, 70, 90, 60, 80. The median is 80, as it is the middle value when the dataset is arranged in ascending order.
What is Range?
The range is a measure of variability that represents the difference between the highest and lowest values in the dataset. It provides an idea of how spread out the data is.
Formula for Range:
Range = Highest value - Lowest value
5 Ways to Master Mean, Mode, Median, and Range
Mastering these statistical concepts requires practice and a deep understanding of their application. Here are five ways to help you master mean, mode, median, and range:
1. Practice with Real-Life Examples
Practice is key to mastering any concept. Use real-life examples, such as exam scores, temperatures, or stock prices, to calculate mean, mode, median, and range. This will help you understand the practical application of these concepts.
2. Use Online Resources and Tools
There are numerous online resources and tools available to help you practice and learn mean, mode, median, and range. Websites like Khan Academy, Coursera, and Stat Trek offer interactive lessons and exercises.
3. Focus on Understanding the Concept, Not Just the Formula
It’s essential to understand the underlying concept behind each measure of central tendency and variability. Don’t just memorize the formulas; take the time to understand what each concept represents and how it is used in real-life scenarios.
4. Learn to Identify Biased and Unbiased Data
Learn to identify biased and unbiased data. For example, a dataset with extreme values or outliers may be biased, affecting the accuracy of the mean.
5. Use Graphical Representations
Graphical representations, such as histograms, box plots, and scatter plots, can help you visualize the data and better understand the measures of central tendency and variability.
📝 Note: Graphical representations can also help you identify biased data and outliers.
Common Mistakes to Avoid
When working with mean, mode, median, and range, it’s essential to avoid common mistakes. Here are a few:
- Calculating the mean incorrectly: Make sure to sum up all the values correctly and divide by the total number of values.
- Confusing mode with median: The mode is the most frequently occurring value, while the median is the middle value when the dataset is arranged in ascending or descending order.
- Ignoring outliers: Outliers can affect the accuracy of the mean and range. Make sure to identify and handle outliers correctly.
Conclusion
Mastering mean, mode, median, and range is essential for anyone working with data. By understanding these fundamental statistical concepts, you can summarize and describe datasets accurately. Remember to practice with real-life examples, use online resources and tools, and focus on understanding the underlying concept behind each measure of central tendency and variability.
What is the difference between mean and median?
+The mean is the average of all values in the dataset, while the median is the middle value when the dataset is arranged in ascending or descending order.
Can a dataset have multiple modes?
+Yes, a dataset can have multiple modes if there are multiple values that appear with the same highest frequency.
What is the range of a dataset?
+The range is the difference between the highest and lowest values in the dataset.
Related Terms:
- Average worksheet pdf
- Corbettmaths mean Median mode
- Mode median mean
- Live worksheet mean median mode
- Mean, median, mode pdf
- Worksheet on central tendency pdf