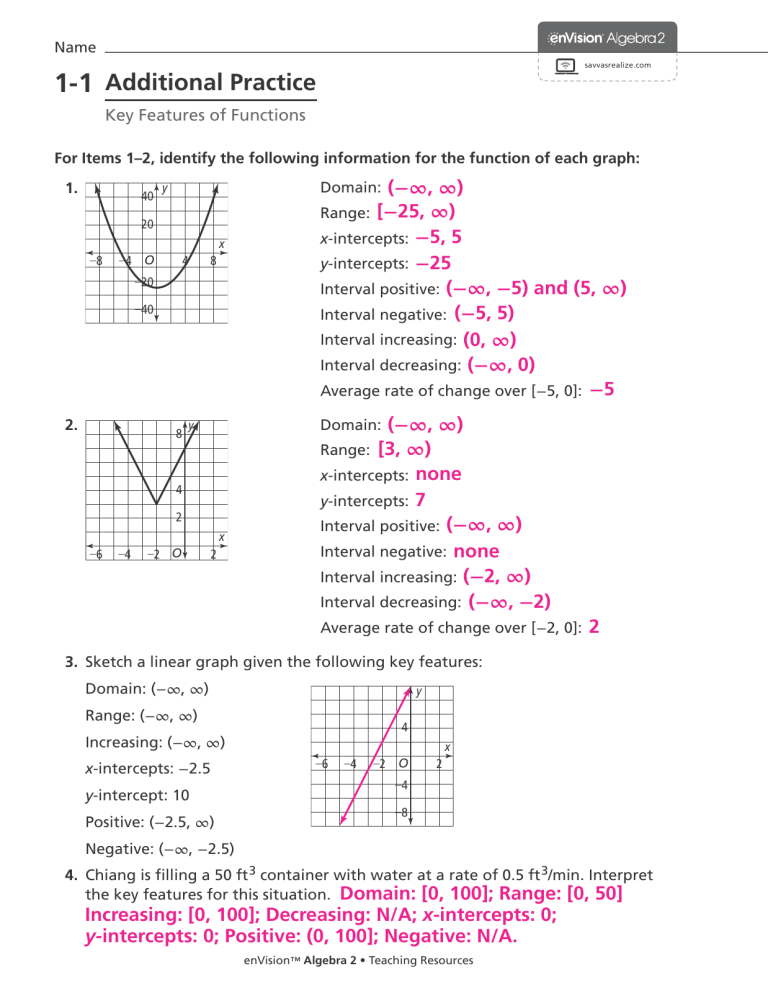
Solve Inequality Word Problems in 5 Easy Steps

Solving Inequality Word Problems: A Step-by-Step Guide
Inequality word problems can be challenging, but breaking them down into manageable steps can make all the difference. Whether you’re a student struggling with math or a professional looking to refresh your skills, this guide will walk you through the process of solving inequality word problems in 5 easy steps.
Step 1: Read and Understand the Problem
The first step in solving an inequality word problem is to read and understand the problem carefully. Take your time to analyze the situation described in the problem, and identify the key elements, such as:
- The unknown quantity ( variable )
- The inequality symbol (e.g., >, <, ≥, ≤)
- The constant values involved
- Any constraints or conditions
Example Problem:
Tom has been saving money for a new bike and has 120 in his savings account. He wants to buy a bike that costs 180. How much more money does Tom need to save each week for 8 weeks to have enough money to buy the bike?
Step 2: Translate the Problem into an Inequality
Once you understand the problem, translate it into an inequality. Use the information gathered in Step 1 to write an inequality that represents the situation.
- Identify the variable (unknown quantity) and assign a symbol to it (e.g., x)
- Write the inequality using the variable, constant values, and inequality symbol
Example Inequality:
Let x be the amount of money Tom needs to save each week. The inequality can be written as:
120 + 8x ≥ 180
Step 3: Solve the Inequality
Now that you have the inequality, solve for the variable. Use algebraic operations to isolate the variable on one side of the inequality.
- Add or subtract the same value to both sides of the inequality to get the variable alone
- Multiply or divide both sides of the inequality by the same value to solve for the variable
Example Solution:
Subtract 120 from both sides of the inequality:
8x ≥ 60
Divide both sides of the inequality by 8:
x ≥ 7.5
Step 4: Check the Solution
After solving the inequality, check your solution to ensure it makes sense in the context of the problem.
- Plug the solution back into the original inequality to verify its validity
- Check for any constraints or conditions that may affect the solution
Example Check:
Plug x = 7.5 back into the original inequality:
120 + 8(7.5) ≥ 180
120 + 60 ≥ 180
180 ≥ 180
The solution x ≥ 7.5 satisfies the inequality.
Step 5: Interpret the Solution
The final step is to interpret the solution in the context of the problem.
- Explain the solution in words, using the context of the problem
- Provide a clear and concise answer to the original question
Example Interpretation:
Tom needs to save at least $7.50 per week for 8 weeks to have enough money to buy the bike.
Important Notes:
- When solving inequality word problems, it’s essential to read the problem carefully and understand the context.
- Use algebraic operations to isolate the variable, and check your solution to ensure it’s valid.
Common Inequality Word Problem Types
Inequality word problems can be categorized into different types, including:
- Linear Inequality Word Problems: These involve solving linear inequalities, where the unknown quantity is a linear expression.
- Quadratic Inequality Word Problems: These involve solving quadratic inequalities, where the unknown quantity is a quadratic expression.
- Rational Inequality Word Problems: These involve solving rational inequalities, where the unknown quantity is a rational expression.
Table: Inequality Word Problem Types
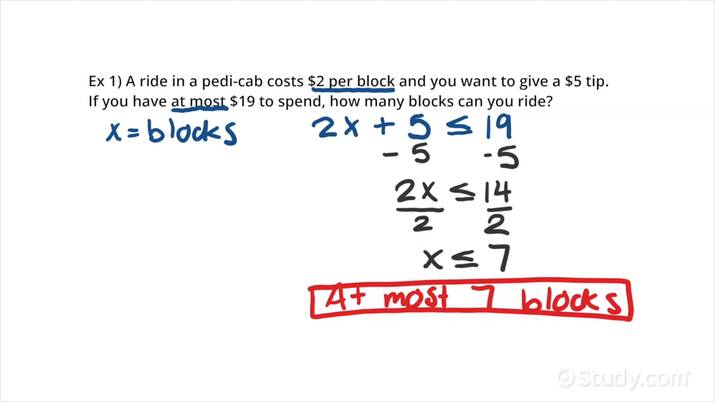
| Inequality Type | Example |
|---|---|
| Linear | 2x + 3 > 5 |
| Quadratic | x^2 + 4x + 4 ≤ 0 |
| Rational | (x + 2)/(x - 1) > 0 |
Frequently Asked Questions
What is the difference between an equation and an inequality?
+An equation is a statement that expresses the equality of two mathematical expressions, whereas an inequality is a statement that expresses the relationship between two mathematical expressions, where one expression is greater than, less than, or equal to the other.
How do I know which type of inequality to use in a word problem?
+The type of inequality used in a word problem depends on the context and the relationship between the variables. Read the problem carefully and identify the key elements, such as the unknown quantity, inequality symbol, and constant values.
Can I use algebraic operations to solve an inequality word problem?
+Yes, you can use algebraic operations, such as addition, subtraction, multiplication, and division, to solve an inequality word problem. However, be careful when multiplying or dividing both sides of the inequality by a negative number, as this can change the direction of the inequality.
By following these 5 easy steps, you’ll be able to solve inequality word problems with confidence. Remember to read the problem carefully, translate it into an inequality, solve for the variable, check your solution, and interpret the solution in the context of the problem. With practice, you’ll become proficient in solving inequality word problems and develop a deeper understanding of mathematical relationships.