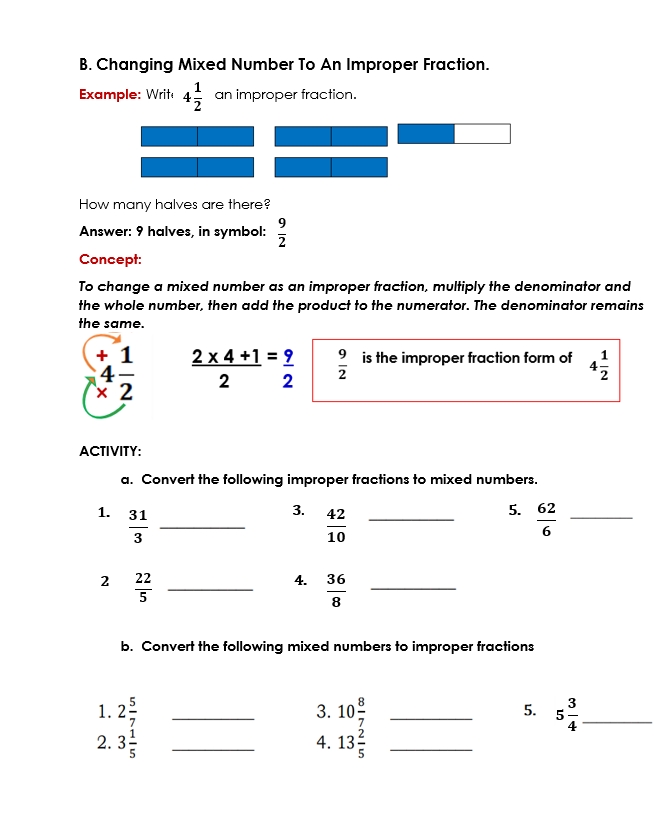
Mastering Probability: Independent and Dependent Events Made Easy
Understanding Probability: A Comprehensive Guide
Probability is a fundamental concept in mathematics and statistics, and it plays a crucial role in various fields, including science, engineering, economics, and finance. In this article, we will delve into the world of probability, focusing on independent and dependent events. By the end of this comprehensive guide, you will have a solid grasp of probability concepts and be able to apply them to real-world problems.
What is Probability?
Probability is a measure of the likelihood of an event occurring. It is a number between 0 and 1, where 0 represents an impossible event and 1 represents a certain event. Probability can be calculated using various methods, including the classical definition, the relative frequency definition, and the subjective definition.
Classical Definition of Probability
The classical definition of probability states that the probability of an event is equal to the number of favorable outcomes divided by the total number of possible outcomes. This definition is often used in games of chance, such as coin tossing and dice rolling.
Relative Frequency Definition of Probability
The relative frequency definition of probability states that the probability of an event is equal to the proportion of times the event occurs in a large number of trials. This definition is often used in statistics and data analysis.
Subjective Definition of Probability
The subjective definition of probability states that the probability of an event is equal to the degree of belief or confidence that the event will occur. This definition is often used in decision-making and risk analysis.
Independent Events
Independent events are events that do not affect each other’s probability of occurring. In other words, the occurrence or non-occurrence of one event does not influence the probability of the other event. Independent events are often represented by the symbol “∩” (intersection).
Example of Independent Events
Tossing two coins is an example of independent events. The probability of getting heads on the first coin is 0.5, and the probability of getting heads on the second coin is also 0.5. The probability of getting heads on both coins is 0.5 x 0.5 = 0.25.
Dependent Events
Dependent events are events that affect each other’s probability of occurring. In other words, the occurrence or non-occurrence of one event influences the probability of the other event. Dependent events are often represented by the symbol “∪” (union).
Example of Dependent Events
Drawing two cards from a deck is an example of dependent events. The probability of drawing a king on the first draw is 4⁄52, and the probability of drawing a king on the second draw depends on the first draw. If the first draw is a king, the probability of drawing a king on the second draw is 3⁄51.
Calculating Probability of Independent Events
The probability of independent events can be calculated using the formula:
P(A ∩ B) = P(A) x P(B)
Where P(A) is the probability of event A, P(B) is the probability of event B, and P(A ∩ B) is the probability of both events occurring.
Calculating Probability of Dependent Events
The probability of dependent events can be calculated using the formula:
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
Where P(A) is the probability of event A, P(B) is the probability of event B, and P(A ∪ B) is the probability of either event occurring.
Table of Probability Formulas
| Formula | Description |
|---|---|
| P(A ∩ B) = P(A) x P(B) | Probability of independent events |
| P(A ∪ B) = P(A) + P(B) - P(A ∩ B) | Probability of dependent events |
| P(A') = 1 - P(A) | Probability of the complement of an event |
📝 Note: The above formulas are essential in calculating probabilities of independent and dependent events. Make sure to understand and apply them correctly to solve problems.
Real-World Applications of Probability
Probability has numerous real-world applications in various fields, including:
- Finance: Probability is used to calculate the risk of investments and portfolios.
- Insurance: Probability is used to calculate premiums and payouts.
- Medicine: Probability is used to calculate the risk of diseases and the effectiveness of treatments.
- Engineering: Probability is used to calculate the reliability of systems and the risk of failures.
Conclusion
Mastering probability is essential in understanding the world around us. By understanding independent and dependent events, you can make informed decisions and calculate the probability of various outcomes. Remember to apply the formulas correctly and use probability in real-world applications.
What is the difference between independent and dependent events?
+Independent events are events that do not affect each other’s probability of occurring, while dependent events are events that affect each other’s probability of occurring.
How do you calculate the probability of independent events?
+The probability of independent events can be calculated using the formula: P(A ∩ B) = P(A) x P(B)
What are some real-world applications of probability?
+Probability has numerous real-world applications in various fields, including finance, insurance, medicine, and engineering.