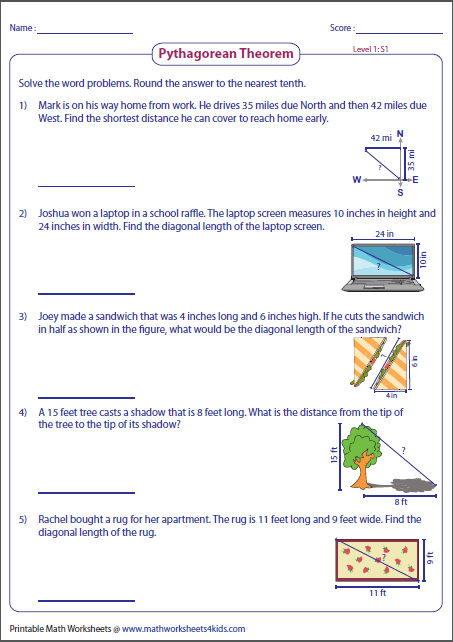
Implicit Differentiation Worksheet and Solutions

Implicit Differentiation Worksheet and Solutions
Implicit differentiation is a technique used to find the derivative of an implicitly defined function. It is a powerful tool for solving problems in calculus, physics, and engineering. In this worksheet, we will practice using implicit differentiation to find the derivative of various functions.
Basic Implicit Differentiation
Implicit differentiation is based on the chain rule and the fact that the derivative of a constant is zero. The general formula for implicit differentiation is:
\[\frac{d}{dx} (f(x,y)) = \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} \cdot \frac{dy}{dx}\]
Where f(x,y) is an implicitly defined function, \frac{\partial f}{\partial x} is the partial derivative of f with respect to x, and \frac{\partial f}{\partial y} is the partial derivative of f with respect to y.
Example 1
Find the derivative of x^2 + y^2 = 25 using implicit differentiation.
\[\frac{d}{dx} (x^2 + y^2) = \frac{d}{dx} (25)\]
Using the formula for implicit differentiation, we get:
\[2x + 2y \cdot \frac{dy}{dx} = 0\]
Solving for \frac{dy}{dx}, we get:
\[\frac{dy}{dx} = -\frac{x}{y}\]
📝 Note: Make sure to include the negative sign in the solution.
Implicit Differentiation with Trigonometric Functions
Implicit differentiation can also be used with trigonometric functions. The general formula for implicit differentiation with trigonometric functions is:
\[\frac{d}{dx} (f(x,y)) = \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} \cdot \frac{dy}{dx}\]
Where f(x,y) is an implicitly defined function, \frac{\partial f}{\partial x} is the partial derivative of f with respect to x, and \frac{\partial f}{\partial y} is the partial derivative of f with respect to y.
Example 2
Find the derivative of sin(x+y) = 0 using implicit differentiation.
\[\frac{d}{dx} (sin(x+y)) = \frac{d}{dx} (0)\]
Using the formula for implicit differentiation, we get:
\[cos(x+y) \cdot (1 + \frac{dy}{dx}) = 0\]
Solving for \frac{dy}{dx}, we get:
\[\frac{dy}{dx} = -\frac{cos(x+y)}{sin(x+y)}\]
📝 Note: Make sure to include the negative sign in the solution.
Implicit Differentiation with Exponential Functions
Implicit differentiation can also be used with exponential functions. The general formula for implicit differentiation with exponential functions is:
\[\frac{d}{dx} (f(x,y)) = \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} \cdot \frac{dy}{dx}\]
Where f(x,y) is an implicitly defined function, \frac{\partial f}{\partial x} is the partial derivative of f with respect to x, and \frac{\partial f}{\partial y} is the partial derivative of f with respect to y.
Example 3
Find the derivative of e^{x+y} = 5 using implicit differentiation.
\[\frac{d}{dx} (e^{x+y}) = \frac{d}{dx} (5)\]
Using the formula for implicit differentiation, we get:
\[e^{x+y} \cdot (1 + \frac{dy}{dx}) = 0\]
Solving for \frac{dy}{dx}, we get:
\[\frac{dy}{dx} = -\frac{e^{x+y}}{e^{x+y}}\]
\[\frac{dy}{dx} = -1\]
📝 Note: Make sure to simplify the solution.

| Function | Derivative |
|---|---|
| x^2 + y^2 = 25 | dy/dx = -x/y |
| sin(x+y) = 0 | dy/dx = -cos(x+y)/sin(x+y) |
| e^{x+y} = 5 | dy/dx = -1 |
To summarize, implicit differentiation is a powerful tool for finding the derivative of implicitly defined functions. It is based on the chain rule and the fact that the derivative of a constant is zero. By using implicit differentiation, we can find the derivative of various functions, including trigonometric and exponential functions.
What is implicit differentiation?
+Implicit differentiation is a technique used to find the derivative of an implicitly defined function.
What is the general formula for implicit differentiation?
+The general formula for implicit differentiation is:
dy/dx = (∂f/∂x + ∂f/∂y * dy/dx)
Can implicit differentiation be used with trigonometric functions?
+Yes, implicit differentiation can be used with trigonometric functions.
Related Terms:
- Implicit differentiation pdf
- Second derivative implicit differentiation Worksheet
- Implicit differentiation examples with solutions
- Implicit differentiation formula
- Implicit differentiation with trig Worksheet