5 Ways to Master Graphing Quadratics
Understanding the Basics of Quadratic Functions
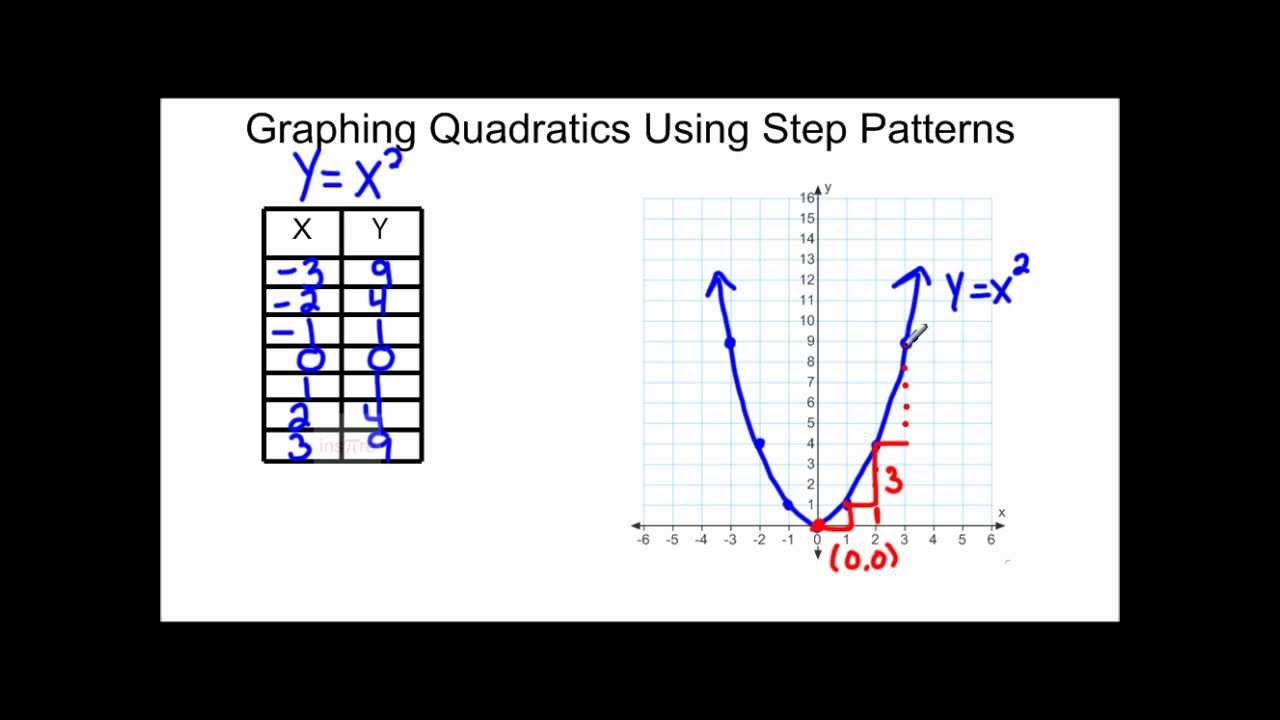
Graphing quadratics is an essential skill for any student of algebra. A quadratic function is a polynomial function of degree two, which means the highest power of the variable (usually x) is two. The general form of a quadratic function is f(x) = ax^2 + bx + c, where a, b, and c are constants, and a cannot be zero. In this article, we will explore five ways to master graphing quadratics, from understanding the basics to advanced techniques.
Way 1: Identify the Key Features of a Quadratic Function
To graph a quadratic function, you need to identify its key features, which include:
- Vertex: The vertex is the lowest or highest point on the graph, depending on the direction of the parabola. It can be found using the formula x = -b/2a.
- Axis of Symmetry: The axis of symmetry is a vertical line that passes through the vertex and divides the graph into two symmetrical parts. Its equation is x = -b/2a.
- Intercepts: The x-intercepts are the points where the graph crosses the x-axis, and the y-intercept is the point where the graph crosses the y-axis.
- Direction of the Parabola: The direction of the parabola depends on the sign of the coefficient a. If a is positive, the parabola opens upwards, and if a is negative, it opens downwards.
📝 Note: To find the vertex, axis of symmetry, and intercepts, you need to have a quadratic function in the standard form f(x) = ax^2 + bx + c.
Way 2: Use the Vertex Form to Graph Quadratics
The vertex form of a quadratic function is f(x) = a(x - h)^2 + k, where (h, k) is the vertex. This form is useful for graphing quadratics because it gives you the vertex and the direction of the parabola immediately.
To graph a quadratic in vertex form:
- Plot the vertex (h, k).
- Determine the direction of the parabola based on the sign of a.
- Use the axis of symmetry to find another point on the graph.
- Plot additional points by substituting x-values into the equation.
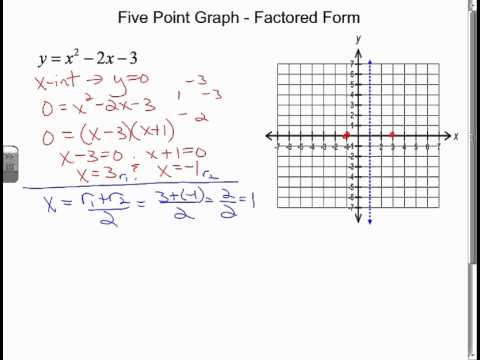
Way 3: Use the Factoring Method to Graph Quadratics
If a quadratic function can be factored, you can use the factoring method to graph it. This method involves factoring the quadratic expression into the product of two binomials.
To graph a quadratic using the factoring method:
- Factor the quadratic expression into the product of two binomials.
- Find the x-intercepts by setting each binomial equal to zero.
- Plot the x-intercepts and the vertex.
- Use the axis of symmetry to find another point on the graph.
| Quadratic Expression | Factored Form | x-Intercepts |
|---|---|---|
| x^2 + 5x + 6 | (x + 2)(x + 3) | x = -2, x = -3 |
Way 4: Use the Graphing Calculator to Visualize Quadratics
A graphing calculator is a powerful tool for visualizing quadratics. It can help you explore the properties of quadratics and check your work.
To use a graphing calculator to visualize quadratics:
- Enter the quadratic function into the calculator.
- Graph the function to visualize its shape.
- Use the calculator to find the vertex, axis of symmetry, and intercepts.
📊 Note: Make sure to set the calculator to the correct mode (e.g., function mode) and adjust the window settings to view the entire graph.
Way 5: Practice, Practice, Practice!
Mastering graphing quadratics requires practice. Try graphing different types of quadratics, such as those with different directions, intercepts, and vertices.
To practice graphing quadratics:
- Choose a quadratic function and identify its key features.
- Graph the function using one of the methods above.
- Check your work using a graphing calculator or by comparing with a graphing app.
- Repeat the process with different quadratic functions.
By following these five ways to master graphing quadratics, you will become proficient in graphing quadratic functions and be able to tackle more complex algebra problems.
In summary, graphing quadratics is an essential skill for algebra students, and mastering it requires understanding the basics, using different graphing methods, and practicing with different types of quadratics. With these five ways, you will be well on your way to becoming a quadratic graphing pro!
What is the standard form of a quadratic function?
+The standard form of a quadratic function is f(x) = ax^2 + bx + c, where a, b, and c are constants, and a cannot be zero.
What is the vertex form of a quadratic function?
+The vertex form of a quadratic function is f(x) = a(x - h)^2 + k, where (h, k) is the vertex.
How do I find the x-intercepts of a quadratic function?
+To find the x-intercepts, set the quadratic function equal to zero and solve for x. This can be done by factoring, using the quadratic formula, or graphing the function.



