Master Quadratic Graphs in 5 Easy Steps
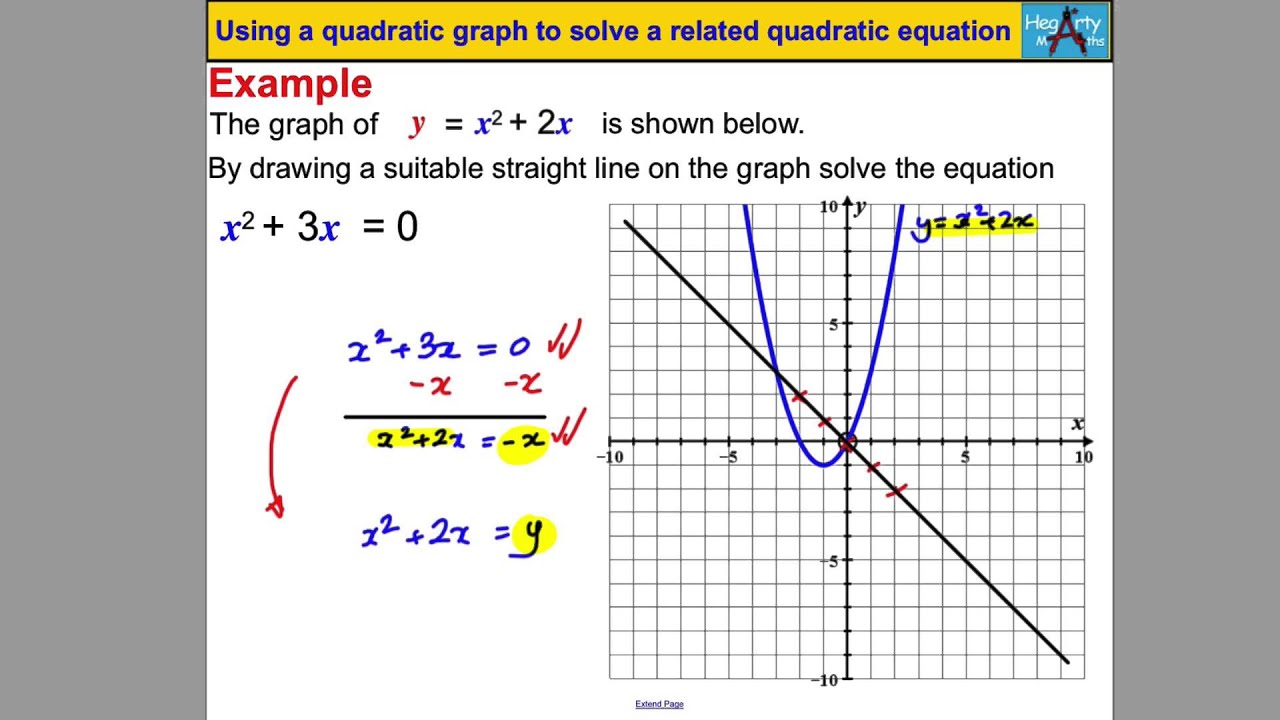
Unlocking the Secrets of Quadratic Graphs
Quadratic graphs are a fundamental concept in mathematics, and understanding them is crucial for solving a wide range of problems in algebra, geometry, and other areas of math. However, many students struggle to grasp the basics of quadratic graphs, leading to frustration and disappointment. In this article, we will break down the process of mastering quadratic graphs into 5 easy steps, making it accessible to anyone who wants to improve their math skills.
Step 1: Understand the Basics of Quadratic Equations
A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable (usually x) is two. The general form of a quadratic equation is:
ax^2 + bx + c = 0
where a, b, and c are constants, and a cannot be zero. The graph of a quadratic equation is a parabola, which is a U-shaped curve that opens upwards or downwards.
📝 Note: It's essential to understand the basics of quadratic equations before diving into graphing.
Step 2: Learn the Different Forms of Quadratic Equations
Quadratic equations can be expressed in different forms, each with its own advantages and disadvantages. The three most common forms are:
- Standard Form: ax^2 + bx + c = 0
- Vertex Form: a(x - h)^2 + k = 0
- Factored Form: (x - r)(x - s) = 0
Understanding these different forms will help you to identify the key features of the graph, such as the vertex, axis of symmetry, and x-intercepts.
Step 3: Identify the Key Features of the Graph
The key features of a quadratic graph are:
- Vertex: The lowest or highest point on the graph, depending on the direction of the parabola.
- Axis of Symmetry: The vertical line that passes through the vertex and divides the graph into two symmetrical halves.
- X-Intercepts: The points where the graph crosses the x-axis.
- Y-Intercept: The point where the graph crosses the y-axis.
These features can be identified using the different forms of the quadratic equation.
Step 4: Graph the Quadratic Equation
Once you have identified the key features of the graph, you can start plotting the points. Here are some tips to keep in mind:
- Plot the vertex: Start by plotting the vertex, which is the lowest or highest point on the graph.
- Plot the x-intercepts: Plot the x-intercepts, which are the points where the graph crosses the x-axis.
- Plot the y-intercept: Plot the y-intercept, which is the point where the graph crosses the y-axis.
- Draw the axis of symmetry: Draw the axis of symmetry, which is the vertical line that passes through the vertex and divides the graph into two symmetrical halves.
Step 5: Analyze and Interpret the Graph
The final step is to analyze and interpret the graph. This involves:
- Identifying the direction of the parabola: Determine whether the parabola opens upwards or downwards.
- Identifying the vertex: Identify the vertex, which is the lowest or highest point on the graph.
- Identifying the axis of symmetry: Identify the axis of symmetry, which is the vertical line that passes through the vertex and divides the graph into two symmetrical halves.
- Identifying the x-intercepts: Identify the x-intercepts, which are the points where the graph crosses the x-axis.
By following these 5 easy steps, you will be able to master quadratic graphs and solve a wide range of problems in algebra and geometry.
What is the standard form of a quadratic equation?
+The standard form of a quadratic equation is ax^2 + bx + c = 0.
What are the key features of a quadratic graph?
+The key features of a quadratic graph are the vertex, axis of symmetry, x-intercepts, and y-intercept.
How do I identify the direction of the parabola?
+The direction of the parabola can be identified by looking at the coefficient of the x^2 term. If it is positive, the parabola opens upwards. If it is negative, the parabola opens downwards.
In conclusion, mastering quadratic graphs is a crucial skill that can be achieved by following these 5 easy steps. By understanding the basics of quadratic equations, learning the different forms, identifying the key features, graphing the equation, and analyzing and interpreting the graph, you will be able to solve a wide range of problems in algebra and geometry. With practice and patience, you will become proficient in graphing quadratic equations and unlock the secrets of this fundamental concept in mathematics.



